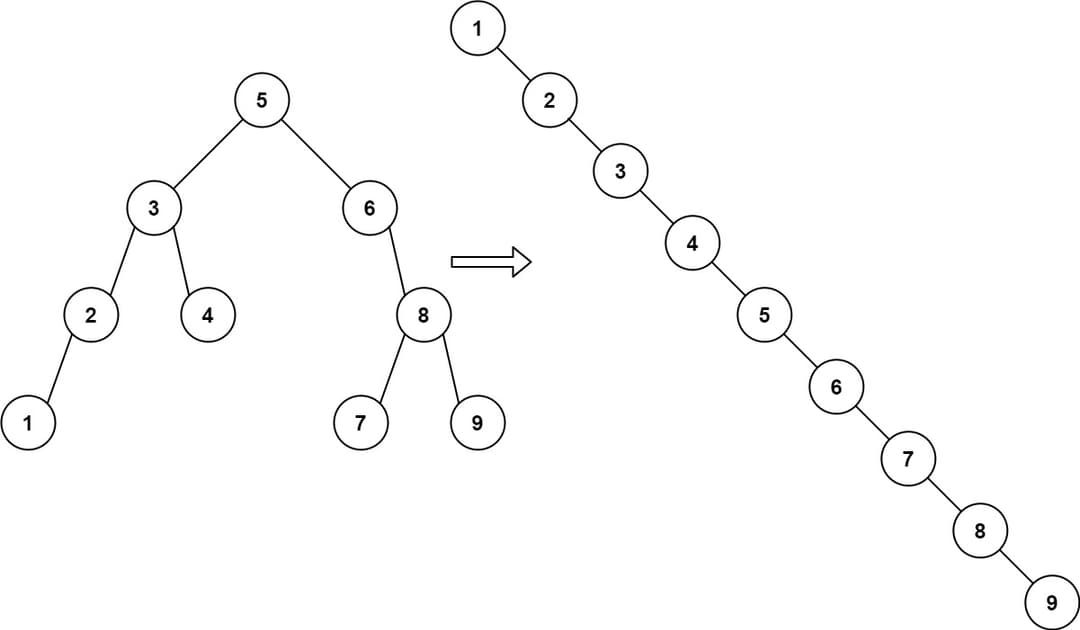
Binary Search Trees
We want to be able to implement a data structure that allows us to store and search for data in an efficient way. To be more specific we want a data structure that only allows us to store data with unique keys, i.e we can’t have duplicates. This matches the requirements for the abstract data type of a dictionary/map, the key uniqueness is also like a set. We want the following operations to be efficient:
- Adding: Add a new element to the data structure. Whilst making sure the key hasn’t been added before.
- Searching: Find an element in the data structure by its key.
- Removing: Remove an element from the data structure by its key.
If we analyze some already known data structures and the run time of their operations we can see that the biggest bottleneck is the search operation to make sure the key is never added twice. Which is why we focus on designing a data structure that makes searching as efficient as possible, the goal would be to have a time complexity of \(O(\log n)\) for all operations.
| Data structure | Adding | Searching | Removing |
|---|---|---|---|
| Unsorted array | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| Sorted array | \(O(n)\) | \(O(\log n)\) | \(O(n)\) |
| Linked list | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| Heap | \(O(\log n)\) | \(O(n)\) | \(O(\log n)\) |
We start of with a similar idea as with implementing a priority queue with a heap. We create a so called binary search tree. This is a binary tree where each node has a key and an element. The idea is that we want to structure the tree in such a way that we can easily search for a specific key. So similar to in a binary search where we make use of the fact that the data is sorted, or in a heap where we make use of the fact that the children are always smaller than the parent, we enforce a similar structure in the binary search tree. This is the so called Search-Tree Property:
For every node \(x\) in the tree, the keys in the left subtree of \(x\) are less than the key of \(x\) and the keys in the right subtree of \(x\) are larger than the key of \(x\).
So in a way we are creating a “stricter” heap, as when searching in the heap we might still have to search through all the elements. The idea with this specific structure is that we can quickly determine if to look in the left or right subtree and therefore removing half of the tree each time we move down a level.
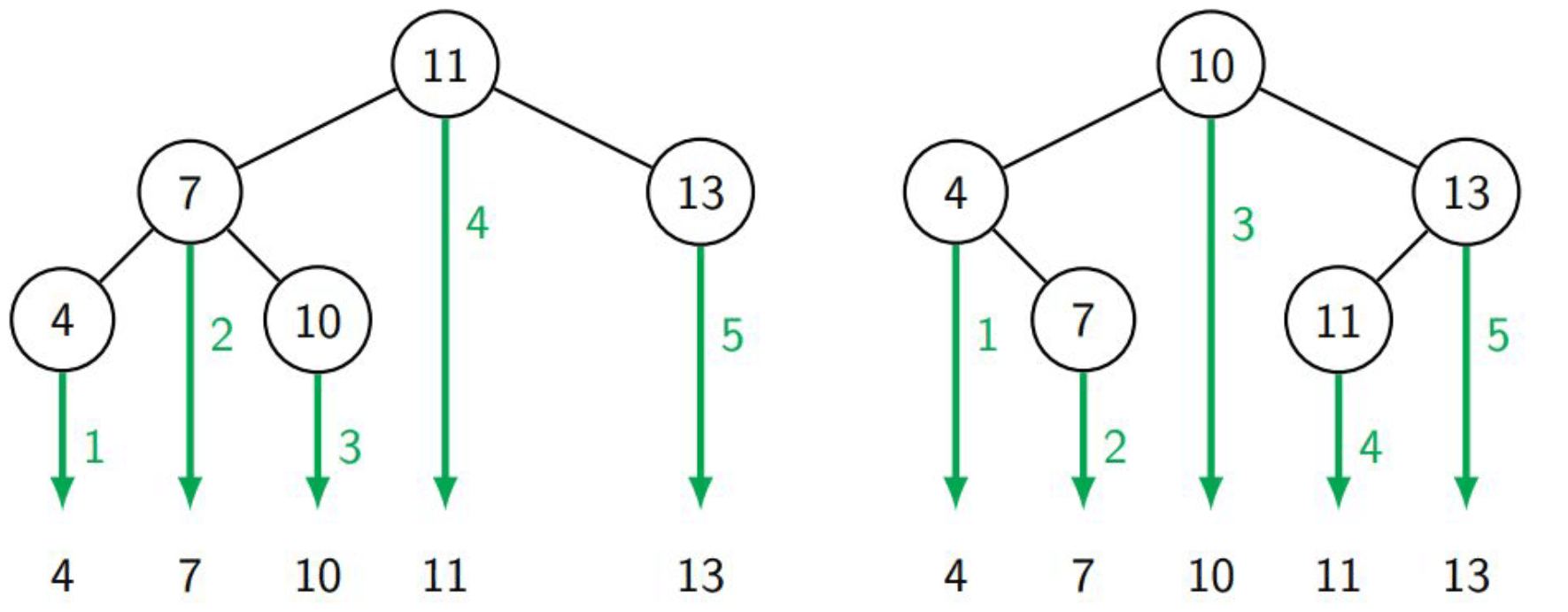
Searching
When searching for a specific key we start at the root and compare the key of the node with the key we are looking for. If the keys are equal we return the element of the node. If the key we are looking for is smaller we move to the left child, if it is larger we move to the right child. We repeat this process until we reach a leaf node. If we reach a leaf node and the key of the leaf node is not equal to the key we are looking for we return null.
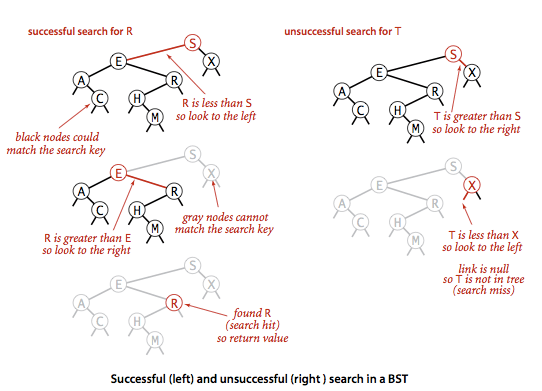
So we can quickly see that the time complexity of the search operation is dependent on the height of the tree so \(O(h)\) where \(h\) is the height of the tree.
public E search(K key, Node<K, E> parent){
// we have not found the key
if (parent == null) {
return null;
}
// the key is found
if (key.compareTo(parent.key)) {
return parent.value;
}
// the key is smaller than the current node
else if (key.compareTo(parent.key) < 0) {
return search(key, parent.left);
}
// the key is larger than the current node
else {
return search(key, parent.right);
}
}Removing
When we want to remove a node there are three cases we need to consider:
- The node is a leaf node, i.e it has no children.
- The node has one child.
- The node has two children.
Let’s start with the easiest case, when the node is a leaf node. Once we have found the node we want to remove we simply remove it from the tree.
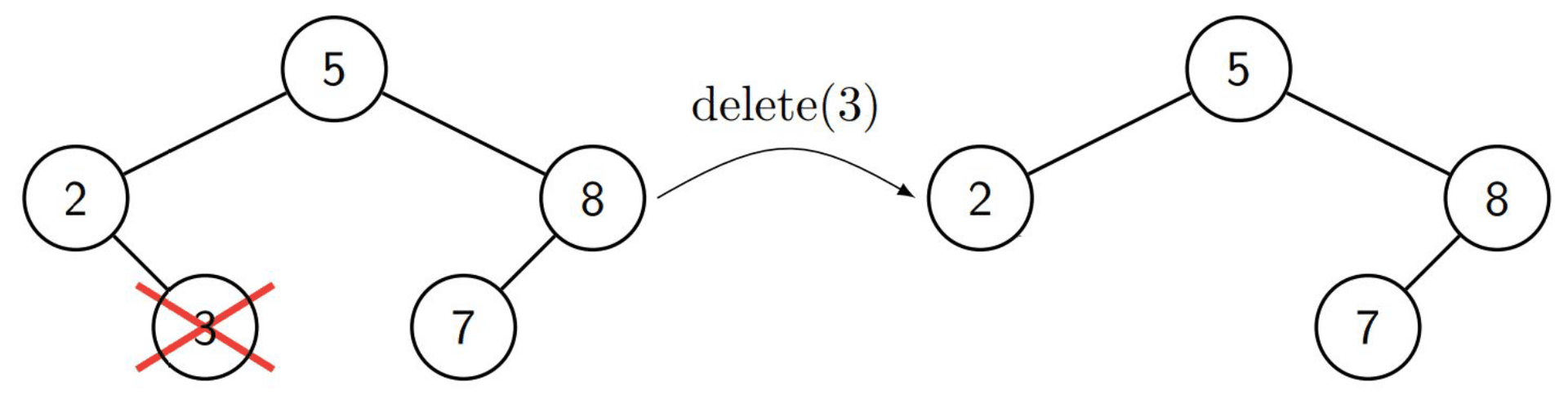
The second case, when the node has one child is also quite simple. We start by finding the node to be removed. We then replace the node with its child.
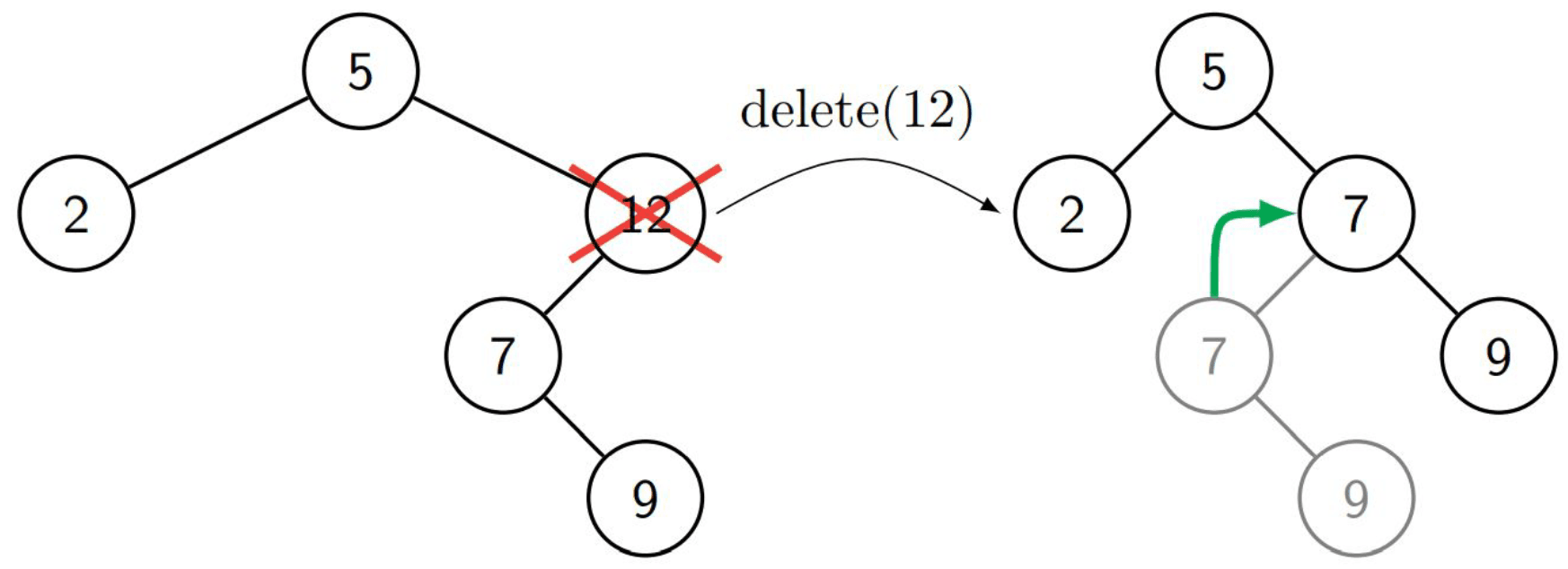
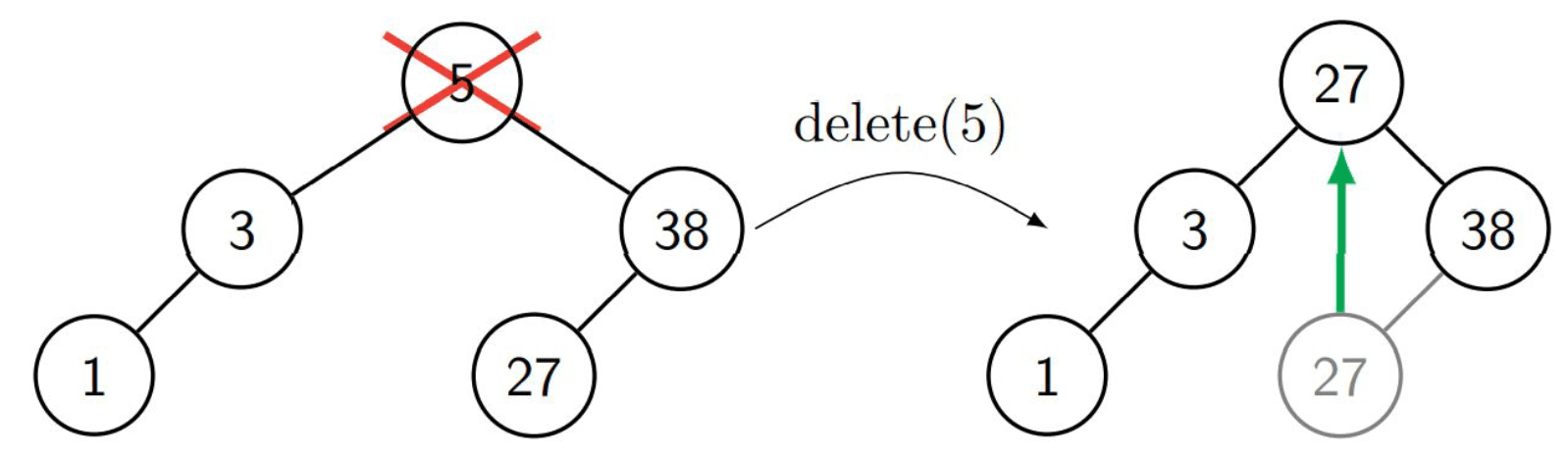
The last case is the most complex as we need to maintain the structure of the tree. We start by finding the node to be removed. However, now we need to find a replacement for the node, the so called successor. In this case we look for the symmetrical successor. This is the node that is “closest” to the node to be removed. The closest node is the node with the smallest key in the right subtree of the node to be removed, so the leftmost node in the right subtree. We then replace the node to be removed with the successor.
public boolean remove(K key, Node<K, E> parent){
// the key is not found
if (parent == null) {
return false;
}
// the key is found
if (key.compareTo(parent.key) == 0) {
// the node is a leaf node
if (parent.left == null && parent.right == null) {
parent = null;
}
// the node has one child
else if (parent.left == null) {
parent = parent.right;
}
else if (parent.right == null) {
parent = parent.left;
}
// the node has two children
else {
Node<K, E> successor = findSuccessor(parent.right);
parent.key = successor.key;
parent.value = successor.value;
// a simple leaf node removal
remove(successor.key, parent.right);
}
return true;
}
// the key is smaller than the current node
else if (key.compareTo(parent.key) < 0) {
return remove(key, parent.left);
}
// the key is larger than the current node
else {
return remove(key, parent.right);
}
}
public Node<K, E> findSuccessor(Node<K, E> parent){
if (parent.left == null) {
return parent;
}
return findSuccessor(parent.left);
}Adding
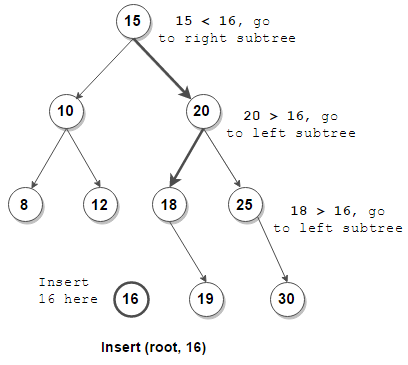
When we want to add a new node to the tree we start at the root and compare the key of the new node with the key of the root. If the new key is smaller we move to the left child, if it is larger we move to the right child. If we find the key already exists during this process we return false. Otherwise we repeat this process until we reach a node that doesn’t have a child in the direction we want to move. We then add the new node as a child of the node we have reached.
public boolean add(K key, E value, Node<K, E> parent){
// the key already exists
if (key.compareTo(parent.key) == 0) {
return false;
}
// the key is smaller than the current node
else if (key.compareTo(parent.key) < 0) {
if (parent.left == null) {
parent.left = new Node<>(key, value);
return true;
}
return add(key, value, parent.left);
}
// the key is larger than the current node
else {
if (parent.right == null) {
parent.right = new Node<>(key, value);
return true;
}
return add(key, value, parent.right);
}
}
This again has a time complexity of \(O(h)\) where \(h\) is the height of the tree. However, you might notice that the structure of the tree and therefore also the height and the time complexity of the operations is dependent on the order in which the elements are added. If we add the elements in a sorted order the tree will become a linked list and the time complexity of the operations will be \(O(n)\). So unfortunately the binary search tree is not enough to guarantee the time complexity of \(O(\log n)\) for all operations. So we need to find some way to keep the tree balanced on both sides. This is where the AVL tree comes in.