Merge Sort

We saw that when searching for an element in a sorted array, we can do it in O(log n) time using a binary search, a divide and conquer algorithm. What if we also tried to sort an array using a divide and conquer strategy? This would result in the merge sort algorithm.

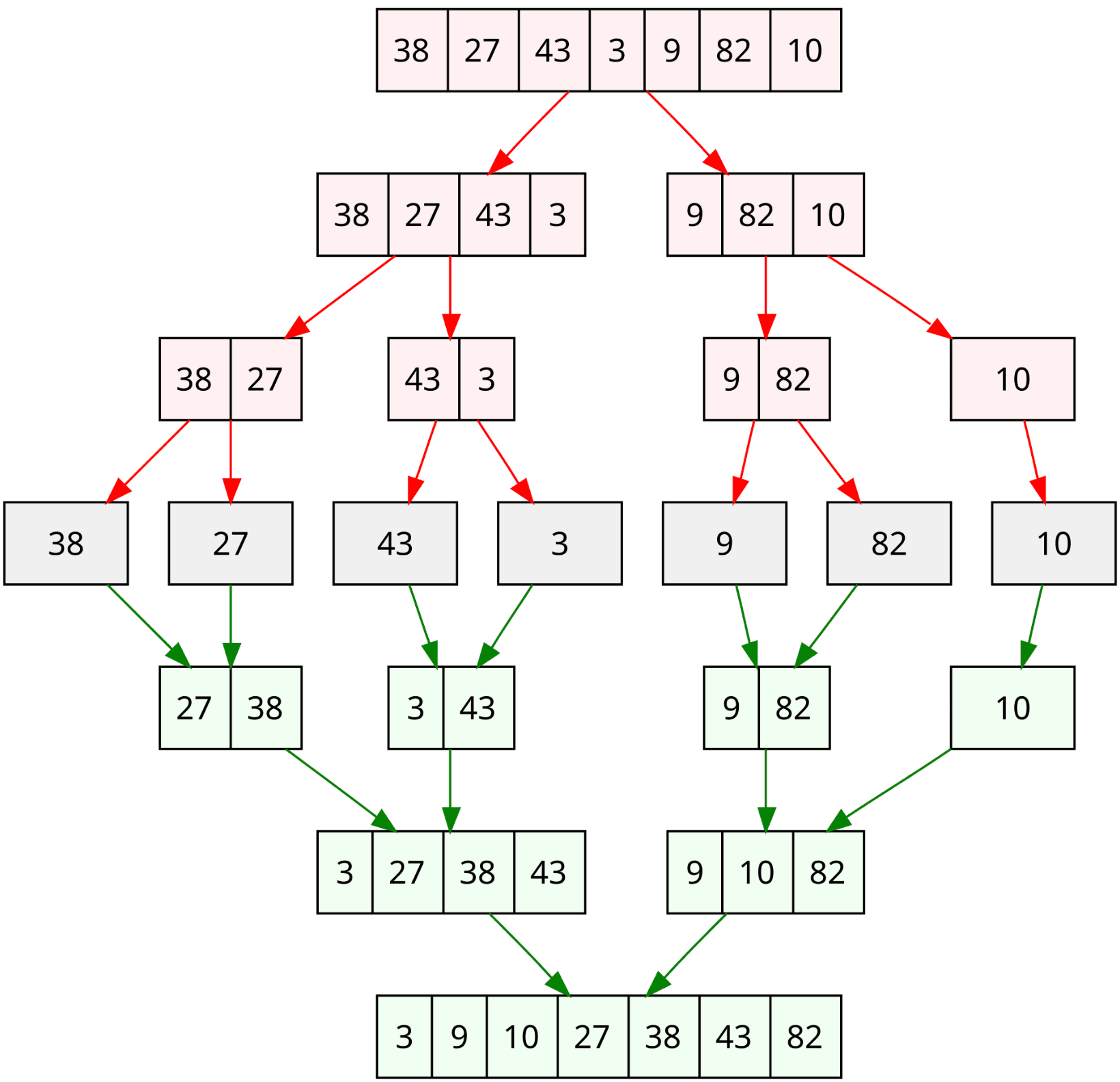
The idea is simple although it is most commonly the first more complex algorithm that students learn. We devide the array in two halves, sort each half and then merge the two sorted halves. However, to sort each half we use recursion. So we keep dividing the array in two halves until we reach the base case of an array of size 1. Then we start merging the arrays back together.

For the merging process we will create a temporary array to store the sorted elements. So to merge two arrays of size 1 we need to compare the two elements and put the smaller one first in the temporary array and then the other one. This way we put them in the correct order. To merge two arrays of size 2 we use the same principle. We compare values of the two arrays and put them in the temporary array in the correct order.

public void mergeSort(int[] arr) {
    // create the temporary array once rather then per call stack
    int[] temp = new int[arr.length];
    mergeSort(arr, temp, 0, arr.length);
}
  
public static void mergeSort(int[] arr, int[] temp, int left, int right) {
    if (right - left > 1) {
        int middle = (left+right)/2;
        mergeSort(arr, temp, left, middle);
        mergeSort(arr, temp, middle, right);
        merge(arr, temp, left, middle, right);
    }
}
  
public static void merge(int[] A, int[] temp, int left, int middle, int right) {
    int i = left;
    int j = middle;
    int k = left;
    while(i < middle && j < right) {
        if (arr[i] < arr[j])
            temp[k++] = arr[i++];
        else 
            temp[k++] = arr[j++];
    }
 
    // take over remaining sections
    while(i < middle) // left
        temp[k++] = arr[i++];
 
    while(j < right) // right
        temp[k++] = arr[j++];
 
    // copy back to original array
    for (int l=left; l < right; l++)
        arr[l] = temp[l];
}

Analysis

Unlike with previous sorting algorithms such as bubble sort or insertion sort, the merge sort algorithm is not in-place. This is because we need to create a temporary array to store the sorted elements. This means that the space complexity of the merge sort algorithm is \(\Theta(n)\) where \(n\) is the size of the original array.

Because we are not working in-place it also no longer makes sense to talk about the number of swaps. Instead, we will look at the number of comparisons and the number of copies.

By analyzing the the code and the visualization we can quickly see that the number of copies per level in the bottom half of the tree is always \(2n\) as the arrays are merged, first they are copied to the temporary array and then back to the original array. So we could conclude that the number of copies is \(2n \log n\) as the tree has \(\log n\) levels.

The number of comparisons can be done in similar fashion, but is slightly more complex as we only count the comparisons that are made between elements, not the comparisons that are made to check if we are done merging. So at the maximum the number of comparisons per level is \(n-1\). This results in a total of \((n-1) \log n\) comparisons.

For a general analysis of the merge sort we can define the following recurrence relation:

where \(d\) is the time it takes to sort an array of size 1, \(cn\) is the time it takes to merge two arrays of size \(n/2\). We avoid having issues with rounding and splitting the collection by assuming that the collection size is a power of 2. So we let \(n = 2^k\) where \(k\) is the number of times we can divide the collection in half.

From the above analysis we could conclude that the time complexity of the merge sort algorithm is \(\Theta(n \log n)\). I will skip proving this matches the recurrence relation using induction, but it is a good exercise to try.

Lower Bound of Comparison Based Sorting

Just like with searching, we also want to know if the merge sort algorithm is the most optimal algorithm using comparisons that we can use to sort a collection.

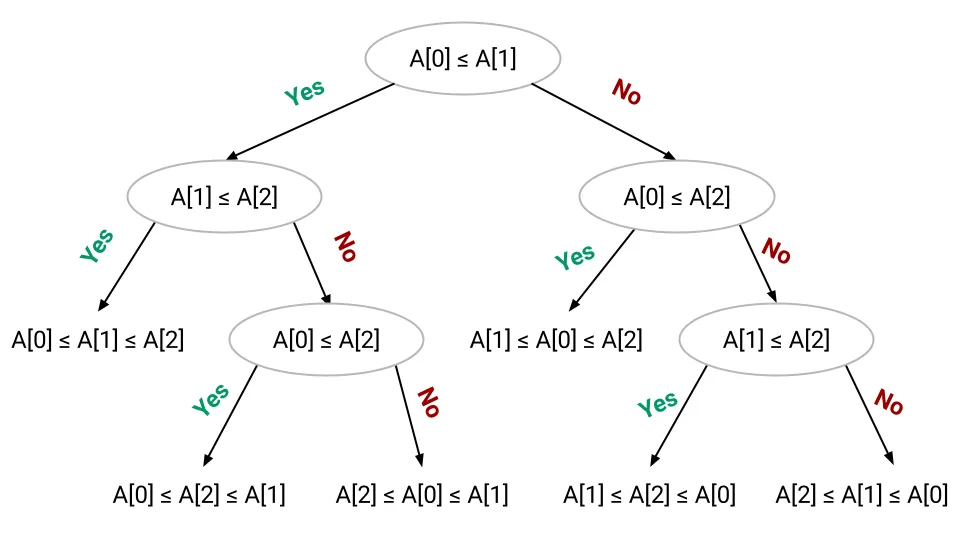
The answer is yes. The lower bound of comparison based sorting is \(\Omega(n \log n)\). This means that the merge sort algorithm is an optimal algorithm in time complexity for comparison based sorting and in \(\Theta(n \log n)\). To prove this, we use the same idea as with searching, an argument from information theory that is based on a decision tree model.

Proof

We design the decision tree just like with the proof of the lower bound of structured search. Each node represents a comparison, so it can be either true or false. This makes the decision tree a binary tree. This leads to each leaf node representing a possible outcome of the sorting, i.e a permutation of the original array. From combinatorics we know that there are \(n!\) possible permutations of an array of size \(n\). Which means we need a binary tree with at least \(n!\) leaf nodes to represent all possible outcomes. A path from the root to a leaf node represents the sorting of the array. Therefore the height of the decision tree represents the worst-case number of comparisons that we have to make to sort the array. So with a height of \(h\), the decision tree has at most \(2^h\) leaf nodes. Therefore the decision tree needs to satisfy the following inequality:

\[n! \text{ permutations} \leq \text{number of leaf nodes} \leq 2^h \]

By solving this inequality, which is a bit more complex than with searching, we can show that the height of the decision tree is \(\Omega(n \log n)\). Therefore the merge sort algorithm is optimal for comparison based sorting in time, however it is not in-place.

Bottom-up Merge Sort

The above method using recursion is called top-down merge sort. There is also a bottom-up merge sort that is iterative.

Natural Merge Sort

trying to take advantage of already sorted parts