Eulerian and Hamiltonian Graphs

This type of walk we now call an Eulerian walk or Eulerian trail (incorrectly called Eulerian path as the vertices can repeat) and is defined as a walk that visits every edge exactly once, hence why it is also called a trail as all edges are unique.

If the walk also starts and ends at the same vertex we call it a closed Eulerian walk, Eulerian tour or Eulerian circuit (incorrectly called Eulerian cycle as the vertices can repeat) where a circuit is just a closed trail.

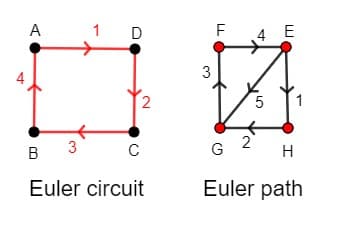
From the example above and through some logical reasoning we can derive the following properties of Eulerian graphs:

• For a graph to be Eulerian it must be connected.
• For a graph to have a Eulerian walk there can either be 0 or 2 vertices with an odd degree (1 vertex with an odd degree is not possible due to the handshake lemma). If there are 0 vertices with an odd degree then the walk can start and end at any vertex. If there are 2 vertices with an odd degree then the walk must start at one of the odd vertices and end at the other. The intuition behind this is that when you enter a vertex you must also leave it and if you have an odd degree then you will have one more edge entering than leaving or vice versa.
• For a directed graph to have a Eulerian walk all vertices must have the same in-degree as out-degre, except for 2 vertices where one has an in-degree one greater than the out-degree and the other has an out-degree one greater than the in-degree. This is intuitivly the same as the above point but for directed graphs.
• For a graph to have a Eulerian tour all vertices must have an even degree. The intuition follows from the above point where you must enter and leave a vertex the same number of times.
• For a directed graph to have a Eulerian tour all vertices must have the same in-degree as out-degree.

To find an Eulerian walk or tour we could try all possible walks but this would result in a time complexity of \(O(n!)\) which is obviously not feasible. So instead we need to come up with a better way. This algorithms is an adaptation of depth-first search. The idea of the algorithm is to start at a vertex and then follow edges until we reach a vertex where we can’t go any further. Depending on the type of graph and the degrees we find when analyzing the graph we should start at a specific vertex, one with odd degree if we have a directed graph and the one with more outgoing edges if we have an undirected graph. When we reach a vertex where we can’t go any further we backtrack to the last vertex where we had other options and continue from there and repeat this process until we have visited all edges. To be able to quickly find the next vertex that still has unvisited edges we can decrease the out-degree every time we take an edge, then when backtracking we just need to check if the out-degree is 0 and if it is we know that we have visited all edges. Everytime we can’t go any further we add the vertex to the front of the walk. Because we only ever visit every edge once but certain vertices multiple times the time complexity of this algorithm is \(O(|V| + |E|)\).

The below version is the same but slightly different by just marking all the edges visited but it works the same way. The reason why these algorithms work is that at the of the first DFS before backtracking we will either be at the end vertex or the start vertex of the Eulerian walk. Due to not being able to go anywhere further and the even degree of the vertices. We then just need to fill in all the “holes”. Does the algorithm have to pick the alphabetically first edge when there are multiple options? Probaly not but it’s a simple way to make the algorithm deterministic.

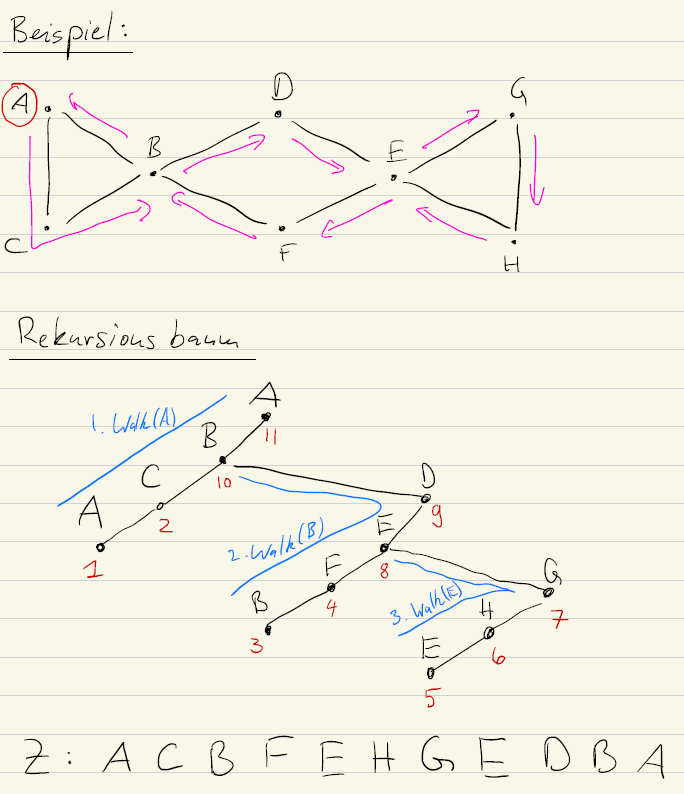
The algorithm below is Hierholzer’s algorithm. By using a stack or doubly linked list we can also code the algorithm iteratively.

Euler(G):
    Empty list Z of Edges
    EulerWalk(G, L, s) // s is the starting vertex
    return Z reversed

EulerWalk(G, Z, v):
    for each edge e not marked in G leaving v to u do
        mark the edge e
        EulerWalk(G, Z, u)
    add v to Z // could also prepend v to Z and then not reverse

Hamiltonian Graphs

The idea of a Hamiltonian path or Hamiltonian cycle Have the same idea as the Eulerian walk or Eulerian tour but instead of visiting every edge once we visit every vertex once. Unfortunatly finding a Hamiltonian path or cycle is NP-complete and can only be solved by brute force. So we would have to try all possible paths or cycles which would result in a time complexity of \(O(n!)\) which is obviously not feasible.

This problem is NP-complete. Another popular version of this problem is the Traveling Salesman Problem (TSP) which is very similar and can be easily reduced to each other. Proper definition of the TSP problem with it being a complete graph and the goal is to find the shortest Hamiltonian cycle. The complete graph is okay as all edges that do not exist can be given a weight of infinity or the maximum weight of the graph plus one.

To check if a graph has a Hamiltonian cycle we can generate all possible hamiltonian cycles which for n vertices is \(\frac{1}{2}(n-1)!\) and then check if all the edges also exist in the graph. This is obviously not feasible for large graphs as it would result in a time complexity of \(O(n!)\).

Can show that for n=20 is more time then the age of the universe?

Using bellman-held-karp algorithm we can solve the problem in \(O(n^2*2^n)\) which is still exponential but much better than \(O(n!)\). This difference can also be shown. And uses dynamic programming and \(O(n * 2^n)\) space.

We can improve this algorithm by using the inclusion-exclusion principle. We basically count all the walks of length n that start and end at a specific vertex. We then sum all these walks and subtract the walks that visit a specific vertex twice. This reuqires only \(O(n^2)\) memory but \(O(n^{2.81} \log n \cdot 2^n)\) time. If we use strassens matrix multiplication to find the walks of length n and iterative squaring. counting the number of Hamiltonian cycles maybe monte carlo algorithm? Is probably not very relevant.

Grid and Bipartite Graphs

for grid graphs there is a hamiltonian cycle if and only if the grid is at least 2x2 and m*n is even. This then also leads to the conclusion that bipartite graphs where the disjoint sets have different sizes can’t have a Hamiltonian cycle.

Hypercubes

Hypercubes have a Hamiltonian cycle.

Diracs Theorem

If a graph has at least 3 vertices and every vertex has a degree of at least n/2 then the graph has a Hamiltonian cycle. The proof of this is rather lengthy but intuitive.

Metric TSP

Is TSP with the additional constraint that the distances between the vertices are a metric. This means that the distance between two vertices is the same in both directions and the triangle inequality holds.

For this problem there exists a 2-approximation algorithm in \(O(n^2)\). A 2-approximation means that the solution is at most twice the optimal solution. So if the optimal solution is a cycle of cost 100 then the algorithm will return a cycle of cost at most 200. The algorithm uses the minimum spanning tree. Double-Tree Algorithm.

There is also a 1.5-approximation algorithm that uses the minimum spanning tree and matchings. Christofides algorithm.