Heap Sort

We have already seen the selection sort algorithm. However, the selection sort algorithm has a time complexity of \(O(n^2)\) which is not as efficient as other sorting algorithms. The bottleneck in the algorithm is that it has to find the smallest/largest element in the array \(n\) times and finding this element takes \(O(n)\) time. But what if we could find the smallest/largest element in \(O(\log n)\) time? This is where the heap sort algorithm comes in.

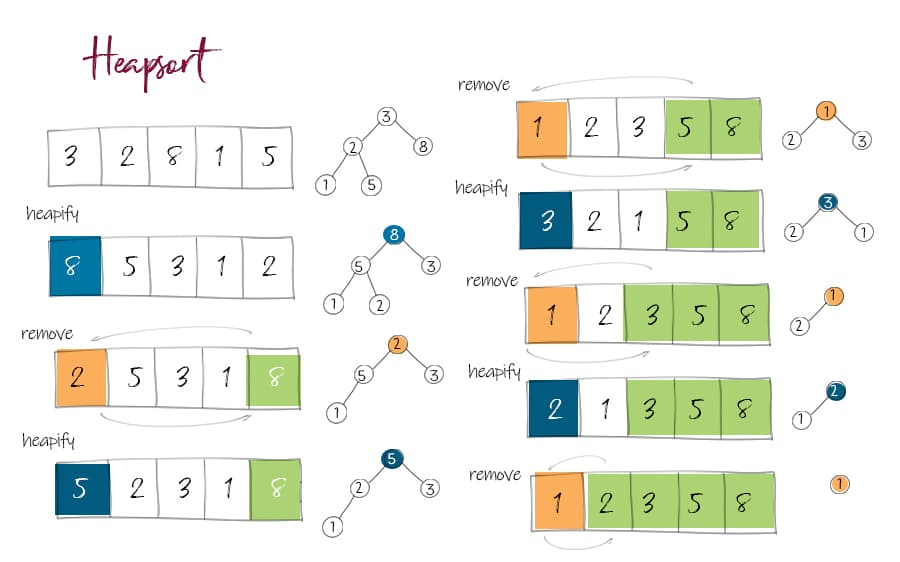
The heap sort algorithm is very simply we first construct a heap from the array in \(O(n \log n)\) time or in \(O(n)\) time if we use Floyd’s construction algorithm. Then we repeatedly remove the root of the heap and place it at the end of the array. This way we have a sorted array in \(O(n \log n)\) time.

public void heapSort(int[] arr) {
    constructMaxHeap(arr);
    for (int i = arr.length - 1; i >= 0; i--) {
        swap(arr, 0, i);
        sinkDown(arr, 0, i);
    }
}