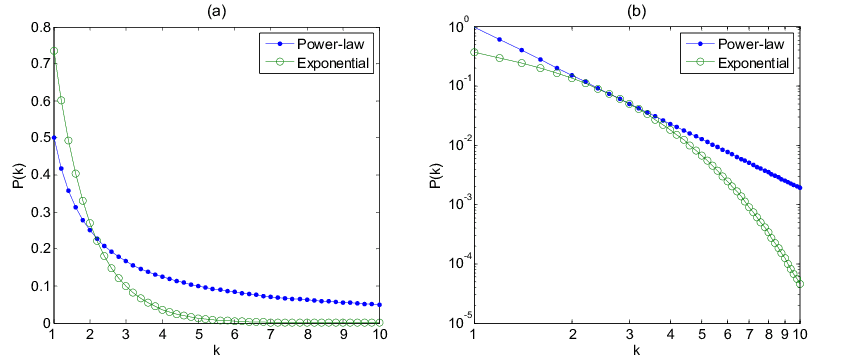
Power Law
The power law defines a relationship between two quantities where a relative change in one quantity \(a\) gives rise to a proportional relative change in the other quantity \(b\). The most common example for this relationship is the area of a square in regard to the length of a side. If the length is doubled then the area is multiplied by a factor of four. A similar example where if the length of a side of a cube is doubled then the volume the cube is multiplied by a factor of eight.
In general, \(x\) and \(y\) are in a power law relationship if \(\log{y}\) is linear to \(\log{x}\).
\[\log{y} = b + a \cdot log{x} \Leftrightarrow y = e^b + x^a \Leftrightarrow y = cx^a \]Power laws are very frequent in our life some common examples are:
- If a person is popular on social network, he/she will get more popular in the future.
- If a person is rich, he/she will get more rich in the future.
A power law can be turned into a linear relationship if the quantities are plotted on logarithmic axes.