Union-Find Data Structure

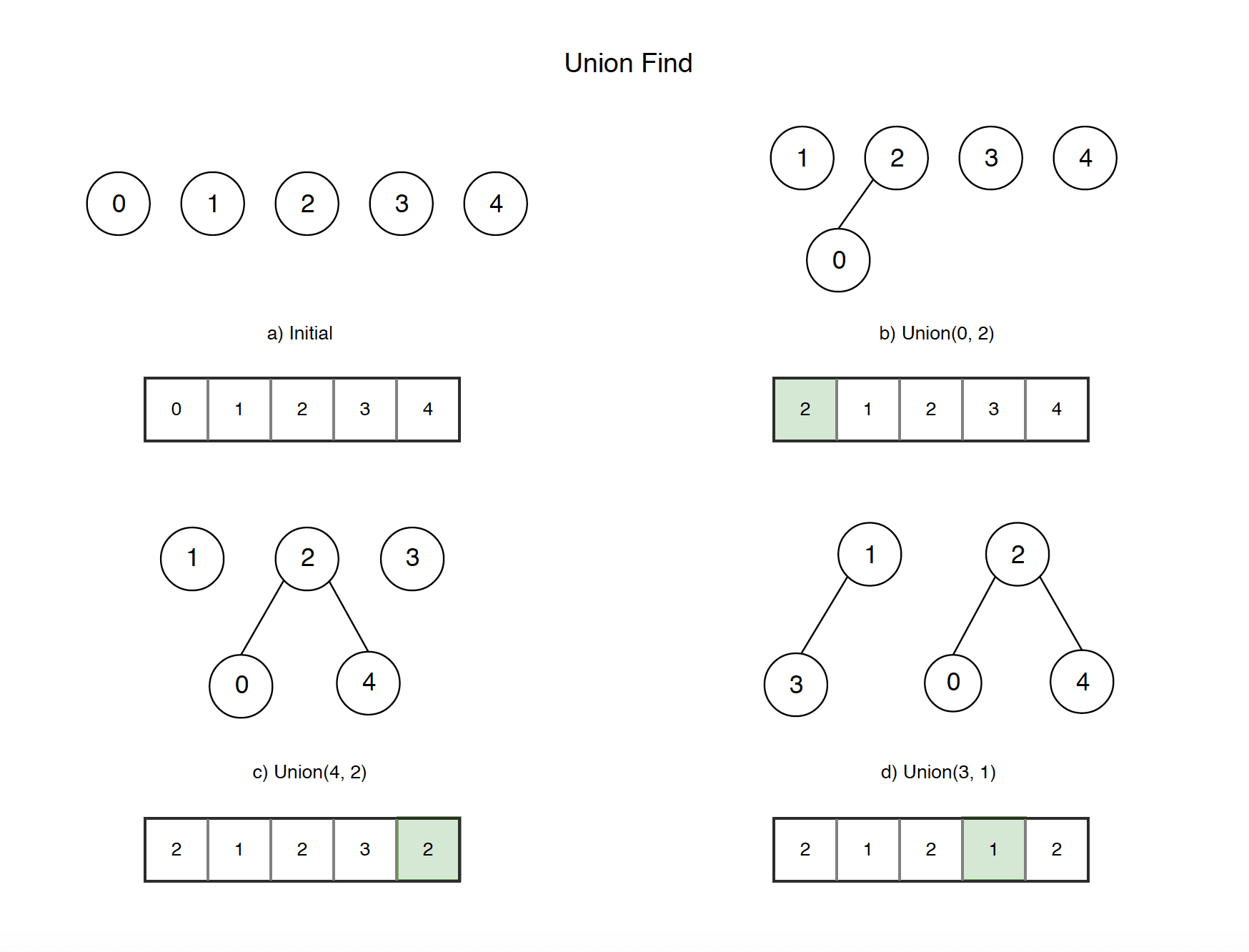
The union-find data structure is a data structure that keeps track of a collection of disjoint sets and efficiently supports two operations, union so joining two disjoint sets and find so finding which set a particular element belongs to. The data structure is very simple each set has a representative element that is used to identify the set so if two elements have the same representative element they are in the same set.

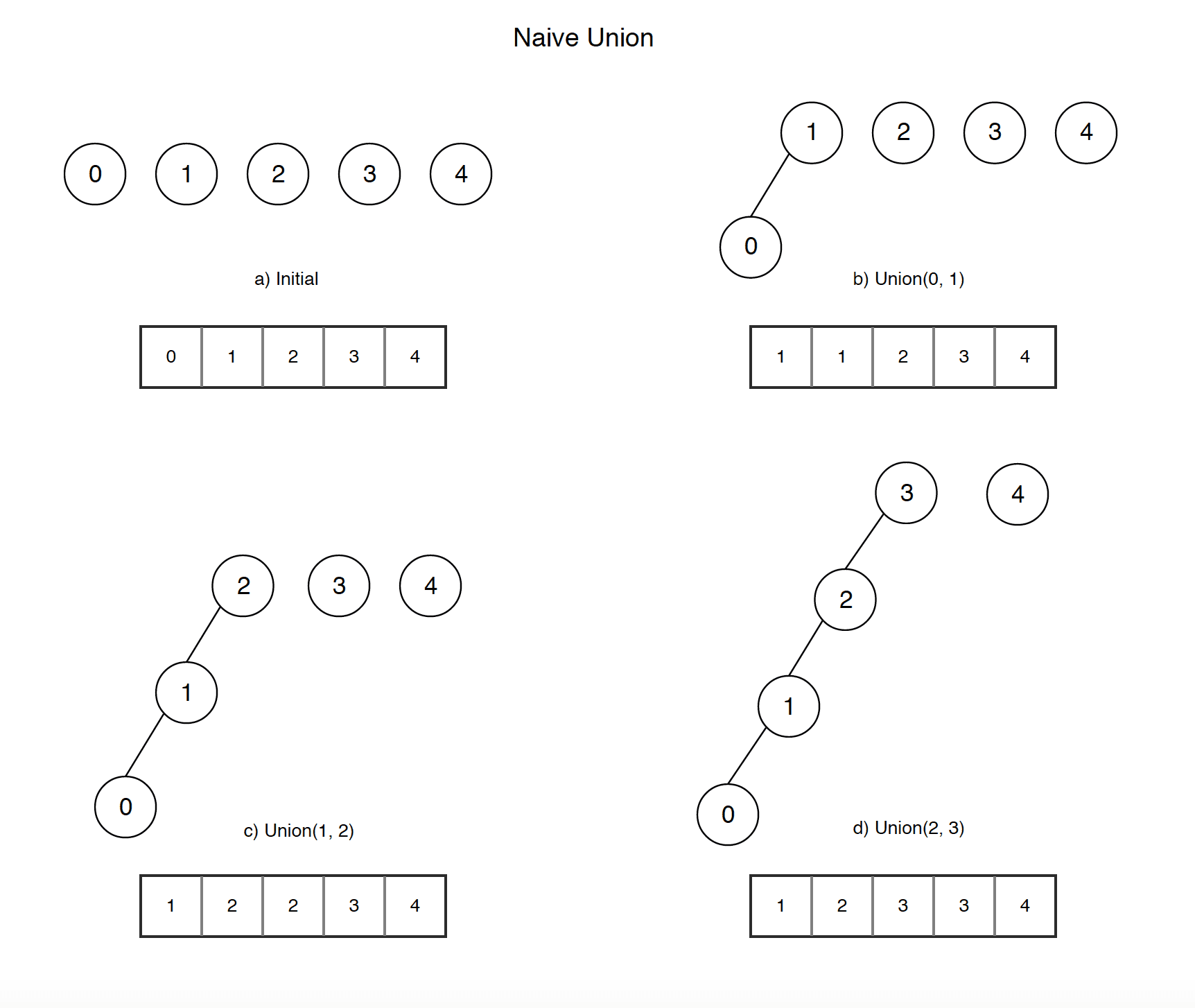
In the beginning each element is its own set so the representative element is itself. This is the key part. The “true” represenative of a set is the element that is the representative of itself. So when we want to find the representative of a set we keep following the representative “tree” until we find the element that is the representative of itself. This can take \(O(n)\) time in the worst case. However, the merge operation can then be done in \(O(1)\) time as we need to do is change the representative element of the one set to the representative element of the other set. So if we have \(n\) elements and we want to merge all of them we have a time complexity of \(O(n^2)\) because the find operations will take \(O(1 + 2 + 3 + \ldots + (n-1)) = O(n^2)\) time.

public class UnionFind {
    private int[] reps;
 
    public UnionFind(int n) {
        reps = new int[n];
        for (int i = 0; i < n; i++) {
            reps[i] = i;
        }
    }
 
    public int find(int a) {
        /* Recursive version
        if (reps[a] != a) {
            return find(reps[a]);
        }
        */
 
        while (reps[a] != a) {
            a = reps[a];
        }
        return a;
    }
 
    public void union(int a, int b) {
        int repA = find(a);
        int repB = find(b);
        reps[repA] = repB;
    }
}

Path Compression

The problem with the above implementation is that the tree of representatives can become very deep and then the find operation can take \(O(n)\) time.

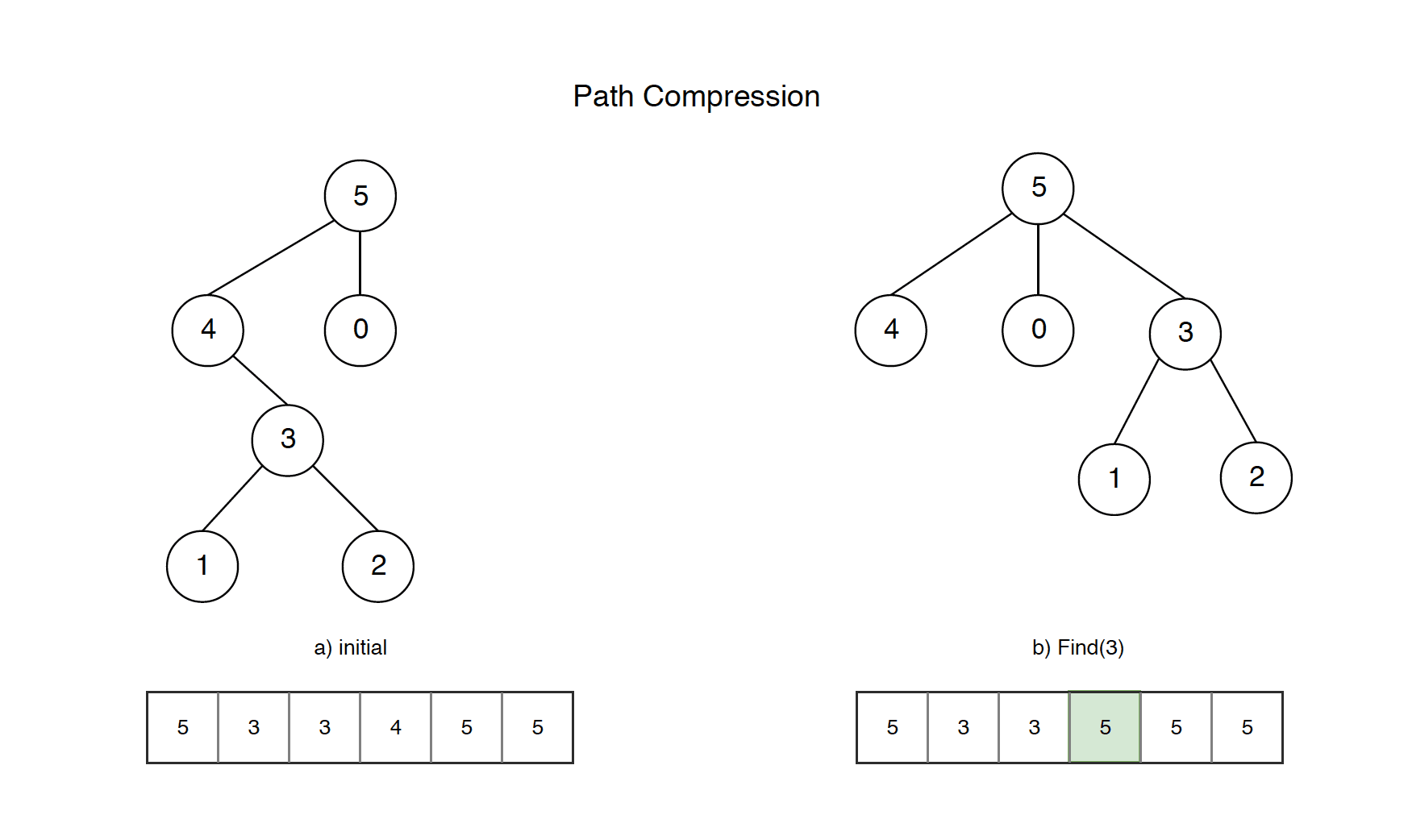
So instead we can use a technique called path compression. The idea is that when a find operation is called and we find the representative of the set on the way back we can set the representative of all the elements on the path to the representative of the set. This way the tree of representatives becomes very flat and the find operation is constant if the initial structure is all elements in their own set.

public int find(int a) {
    if (reps[a] != a) {
        reps[a] = find(reps[a]); // path compression
    }
    return reps[a];
}

Union by Rank or Size

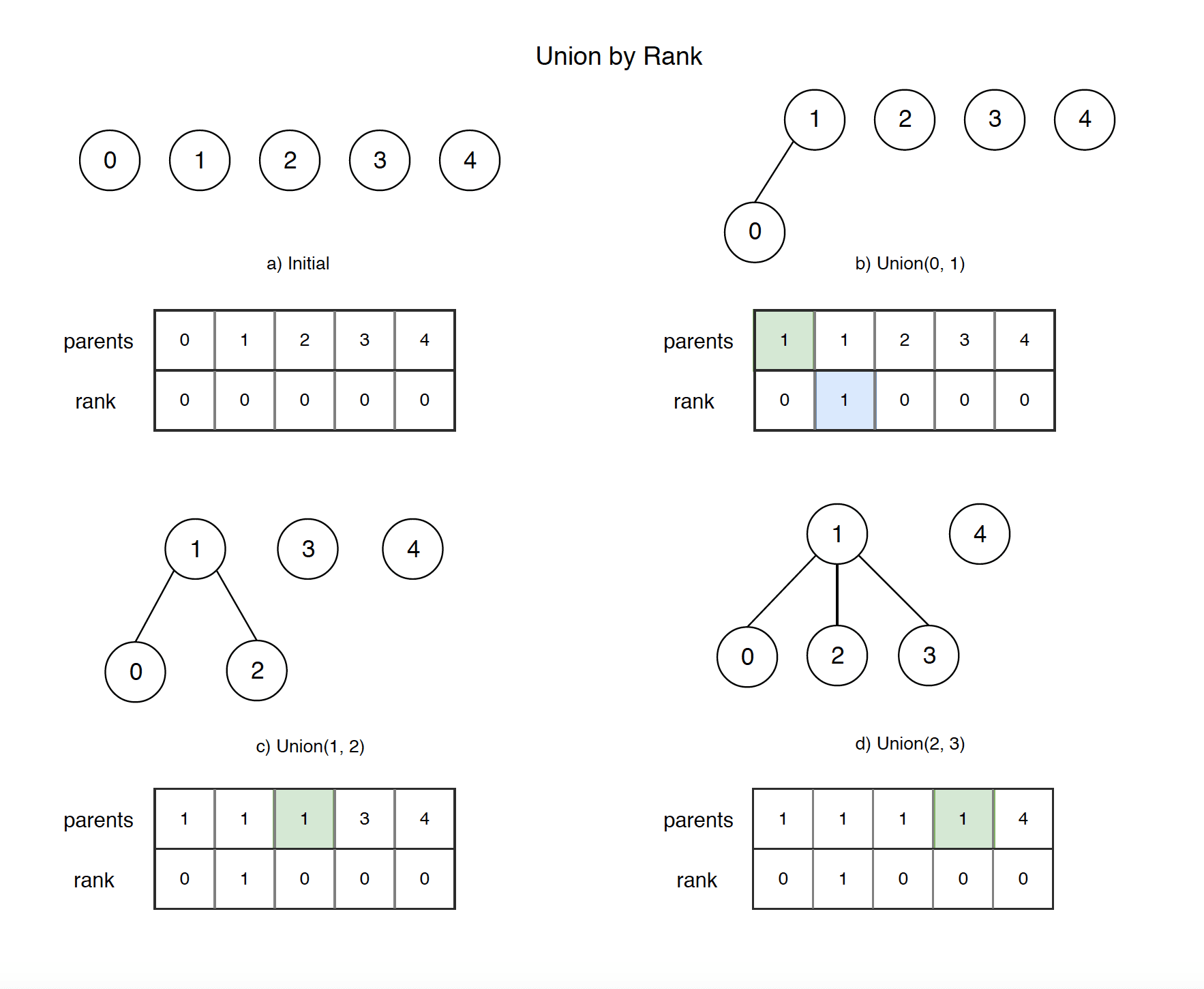
Another optimization we can do is to keep track of the rank of the set. The rank of a set is the depth of the subtree rooted at the representative. So when we merge two sets we can then merge the set with the smaller rank into the set with the larger rank. This way the tree of representatives stays flat. You can also use the size of the set rather then the rank but it comes down to the same thing. This way it is clear that the worst case for the union is \(O(\log n)\) so the time complexity for merging all elements is \(O(n \log n)\).

public class UnionFind {
    private int[] reps;
    private int[] ranks;
 
    public UnionFind(int n) {
        reps = new int[n];
        ranks = new int[n];
        for (int i = 0; i < n; i++) {
            reps[i] = i;
            ranks[i] = 0;
        }
    }
 
    public int find(int a) {
        if (reps[a] != a) {
            reps[a] = find(reps[a]); // path compression
        }
        return reps[a];
    }
 
    public void union(int a, int b) {
        int repA = find(a);
        int repB = find(b);
        if (repA == repB) {
            return;
        }
        if (ranks[repA] < ranks[repB]) {
            reps[repA] = repB;
        } else if (ranks[repA] > ranks[repB]) {
            reps[repB] = repA;
        } else {
            reps[repA] = repB;
            ranks[repB]++;
        }
    }
}

Using Union-Find to Detect Cycles in a Graph