All Pairs Shortest Path
We have seen that to find the shortest path between two vertices \(s\) and \(t\) the time complexity is the same as for finding all of the shortest paths starting at \(s\). This is called single source shortest path problem as we just have the single source \(s\) or one-to-all shortest path problem. But what if we want to find the shortest path between all pairs of vertices in a graph? This is called the all pairs shortest path problem.
One simple idea to solve this problem is to just run a shortest path algorithm starting at each vertex in the graph.
| Weights | Algorithm | one-to-all | all-to-all |
|---|---|---|---|
| Same positive weight or no weight | BFS | \(O(m + n)\) | \(O(n(m + n))\) |
| Non-negative weights | Dijkstra with Fibonacci Heap | \(O(m + n \log n)\) | \(O(n(m + n \log n))\) |
| Real weights | Bellman-Ford | \(O(mn)\) | \(O(n^2m)\) |
| Real weights | Floyd-Warshall | - | \(O(n^3)\) |
| Real weights | Johnson | - | \(O(n(m + n \log n))\) |
Important for the Bellman-Ford algorithm is that it can handle negative weights but not negative cycles. If there is a negative cycle in the graph then we say that there is no shortest path between the vertices in the graph.
The goal is now to find the shortest path between all pairs of vertices in a graph with real weights in less than \(O(n^m)\) time.
Floyd-Warshall Algorithm
The algorithm of Floyd-Warshall is a dynamic programming algorithm that finds the shortest path between all pairs of vertices in a graph with real weights in \(O(n^3)\) time. Just like all other shortest path algorithms it does not work with negative cycles. The algorithm uses a 3-dimensional array \(D\) with each dimension being the number of vertices in the graph. The idea is to build up the shortest path between all pairs of vertices by adding one vertex at a time to the path:
\[D[u,v,k] = \text{shortest path from } u \text{ to } v \text{ using only the vertices } 1, 2, \ldots, k \]We can then define three possible scenarios for a path from \(u\) to \(v\) using the vertices \(i\):
- The shortest path goes from \(u\) to \(v\) without using the vertex \(i\). In this case the shortest path is the same as the shortest path from \(u\) to \(v\) using only the vertices \(1, 2, \ldots, i-1\) so \(D[u, v, i] = D[u, v, i-1]\).
- The shortest path goes from \(u\) to \(v\) using the vertex \(i\) as an intermediate vertex. In this case the shortest path is the shortest path is then \(D[u,v,i] = D[u,i,i-1] + D[i,v,i-1]\).
- The shortest path goes from \(u\) to \(v\) using the vertex \(i\) multiple times. In this case we would have a negative cycle in the graph as there is no other motivation to use the vertex \(i\) multiple times. So we can ignore this case.
So to calculate the shortest path between all pairs of vertices in a graph we take the minimum of the two cases above:
\[D[u,v,k] = \min(D[u,v,k-1], D[u,k,k-1] + D[k,v,k-1]) \]The base case is when we go over no intermediate vertices so \(D[u,v,0] = w(u,v)\) where \(w(u,v)\) is the weight of the edge between the vertices \(u\) and \(v\). If there is no edge between the vertices \(u\) and \(v\) then \(D[u,v,0] = \infty\) and if \(u = v\) then \(D[u,v,0] = 0\). Putting this all together we get the following algorithm:
public int[][] floydWarshall(List<List<Integer> graph, List<List<Integer>> weights) {
int n = graph.size();
int[][][] D = new int[n][n][n];
// base cases
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
D[i][j][0] = 0;
} else {
D[i][j][0] = Integer.MAX_VALUE;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < graph.get(i).size(); j++) {
int u = i;
int v = graph.get(i).get(j);
D[u][v][0] = weights.get(i).get(j);
}
}
// calculate the shortest path between all pairs of vertices
for (int k = 1; k < n; k++) {
for (int u = 0; u < n; u++) {
for (int v = 0; v < n; v++) {
D[u][v][k] = Math.min(D[u][v][k-1], D[u][k][k-1] + D[k][v][k-1]);
}
}
}
// extract the shortest paths from the 3-dimensional array
int[][] shortestPaths = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
shortestPaths[i][j] = D[i][j][n-1];
// check for negative cycles
if (i == j && D[i][j][n-1] < 0) {
return null;
}
}
}
return shortestPaths;
}Notice that if on the diagonal of the matrix so \(u = v\) we have a negative value then there is a negative cycle in the graph. This is because the shortest path from a vertex to itself should always be 0 unless there is a shorter path that goes through a negative cycle.
Johnson’s Algorithm
Johnson’s idea was to be able to use Dijkstra’s algorithm for the all pairs shortest path problem for graphs with real weights giving us a all-to-all shortest path problem in \(O(n(m + n \log n))\) time. The idea is to transform the graph so that all the weights are non-negative without changing the shortest path between the vertices and then run Dijkstra’s algorithm for each vertex in the graph.
The first transformation I would come up with to make all the weights non-negative is to find the edge with the smallest weight and then add the absolute value of that weight to all the edges in the graph. This would make all the weights non-negative. The question is if this transformation would change the shortest path between the vertices. The answer is unfortunately yes. The reason being that paths that go over more edges are impacted more by the transformation than paths that go over fewer edges even if they have previously been the shortest path.
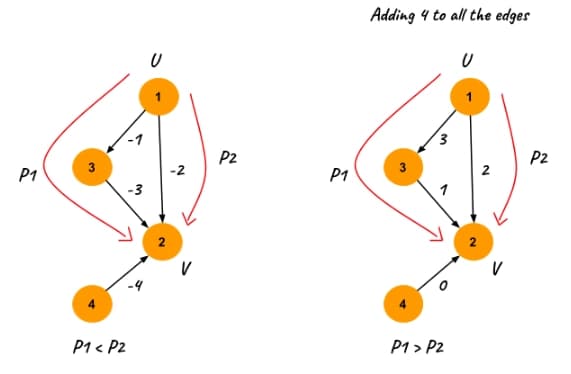
So instead we want to add some value to the weights so that all the paths from \(u\) to \(v\) change by the same amount. The idea here is to add some value which is often called the potential or height of the vertices.
\[\hat{w}(u, v) = w(u, v) + h(u) - h(v) \]We can show that all paths from \(u\) to \(v\) change by the same amount with the following equations where we look at the weights of a path from \(u\) to \(v\) that goes over the vertices \(u = u_0, u_1, \ldots, u_k = v\). The reason being that the additions and subtractions of the heights cancel each other out apart from the first and last vertex.
\[\begin{align*} w(u \rightarrow v) & = \sum_{i=0}^{k-1} w(u_i, u_{i+1}) \\ \hat{w}(u \rightarrow v) & = \sum_{i=0}^{k-1} \hat{w}(u_i, u_{i+1}) \\ & = \sum_{i=0}^{k-1} (w(u_i, u_{i+1}) + h(u_i) - h(u_{i+1})) \\ & = \sum_{i=0}^{k-1} w(u_i, u_{i+1}) \quad + h(u_0) - h(u_k) \\ & = \sum_{i=0}^{k-1} w(u_i, u_{i+1}) \quad + h(u) - h(v) \end{align*} \]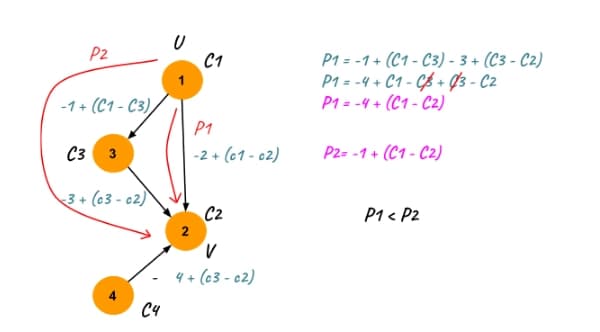
The question is now how to define the heights of the vertices. Important is that the resulting weights are non-negative so:
\[\hat{w}(u, v) = w(u, v) + h(u) - h(v) \geq 0 \]Johnson’s idea was to add a vertex \(z\) to the graph and add edges from \(z\) to all the other vertices in the graph with weight 0. The height of a vertex he then defined as the shortest path from \(z\) to the vertex.
\[h(v) = d(z, v) = \text{shortest path from } z \text{ to } v \]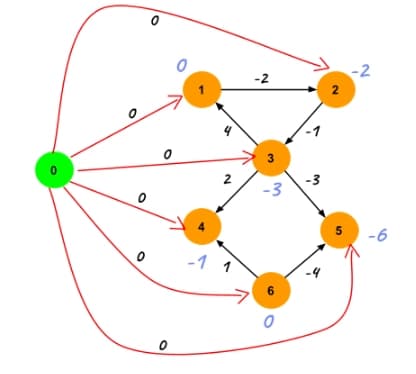
This results in the fact that all heights are either 0 or negative. The vertices that normally within the graph would have a positive shortest path now have shortest path of 0 and all the other vertices have negative shortest paths. So we can then say the following for all edges \((u, v)\) in the graph:
\[\begin{align*} h(v) \leq h(u) + w(u, v) \\ w(u, v) + h(u) - h(v) \geq 0 \\ \hat{w}(u, v) \geq 0 \end{align*} \]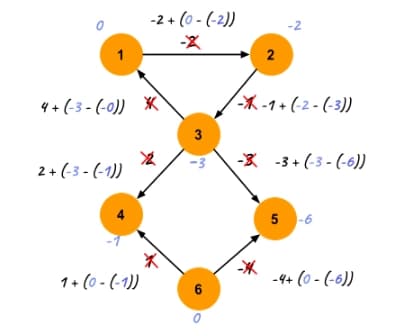
why does the first inequality hold?
This results in a rather simple algorithm for finding the shortest path between all pairs of vertices in a graph with real weights. We add the vertex \(z\) to the graph and add edges from \(z\) to all the other vertices with weight 0 in \(O(n)\) time. We then run Bellman-Ford on the graph for the vertex \(z\) in \(O(nm)\) time. So if there are negative cycles the will be detected in this step and we can return that there is no shortest path between the vertices in the graph. We then update the weights of the edges in the graph so that they are all positive and then run Dijkstra’s algorithm for each vertex in the graph in \(O(n(m + n \log n))\) time but now being able to handle real weights.
public int[][] johnson(List<List<Integer> graph, List<List<Integer>> weights) {
// add vertex z to the graph
int z = graph.size();
for (int i = 0; i < graph.size(); i++) {
graph.get(z).add(i);
weights.get(z).add(0);
}
// run Bellman-Ford on the graph for the vertex z
int[] h = bellmanFord(graph, weights, z);
// update the weights of the edges in the graph
for (int i = 0; i < graph.size(); i++) {
for (int j = 0; j < graph.get(i).size(); j++) {
int u = i;
int v = graph.get(i).get(j);
weights.get(i).set(j, weights.get(i).get(j) + h[u] - h[v]);
}
}
int[][] shortestPaths = new int[graph.size()][graph.size()];
for (int i = 0; i < graph.size(); i++) {
shortestPaths[i] = dijkstra(graph, weights, i);
}
return shortestPaths;
}All Pairs Reachability
add self loop to the graph and just keep multiply the adjacency matrix \(n-1\) times with itself. The idea of the self looping is to be able to wait at a vertex? The repeatedly multiplying the adjacency matrix with itself can be done using multiplication by squaring to get the time complexity down to \(O(n^3 \log n)\) where \(n^3\) is the cost of a matrix multiplication and \(\log n\) is the number of times we have to multiply the matrix with itself rather than multiplying the matrix with itself \(n-1\) times.
Number of Triangles
A triangle is a cycle of length 3 in a graph. So if we cube the adjacency matrix of a graph we get the number of paths of length 3. If we then look at the diagonal of the matrix we get the number of triangles in the graph as these are the paths that start and end at the same vertex. But because each triangle counts 3 times for each of the points in the triangle we have to divide the number of paths of length 3. The trace is then just the sum of the diagonal of the matrix.
\[\text{Number of triangles} = \sum_{i=1}^n A_G^3[i][i] / 3 = \text{trace}(A_G^3) / 3 \]Number of Squares
Not as easy as the number of triangles because there are multiple ways to form a square?