Topological Ordering

If we are given a directed graph where each edge signifies a dependency between two vertices. So if there is an edge \(e\) from the vertex \(a\) to the vertex \(b\) then \(b\) depends on \(a\), in other words \(a\) has to be processed before \(b\). If we have a graph like this then the goal of finding a topological oder or also often called topological sorting is to find an order for the vertices so that one can process them in that order and all dependencies are fulfilled.

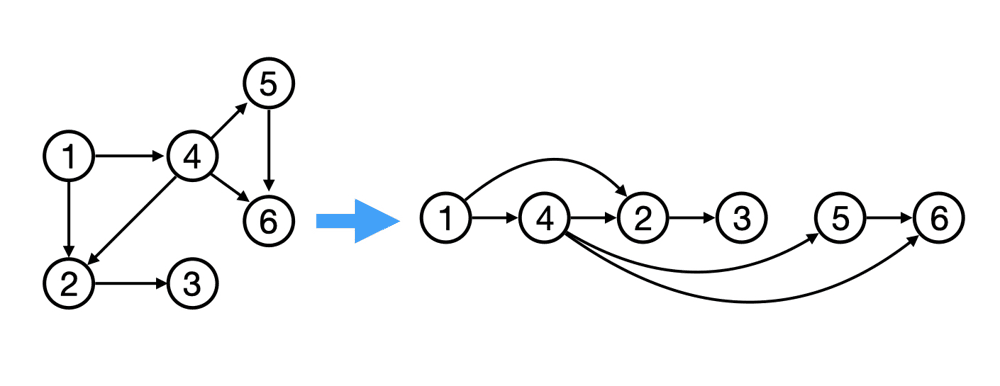
There are a few properties of a topological order that we can quickly notice from the above example:

• Acyclic: A graph has a topological order if and only if it is acyclic. If there is a cycle in the graph then there is no way to order the vertices in a way that all dependencies are fulfilled. As there would then always be a vertex that depends on a vertex that is later in the order.
• Sink: Because the graph has to be acyclic there has to be at least one vertex that has no outgoing edges, a so called sink, our path has to stop somewhere. This is then a possible end point for our topological order.
• **Source: Because the graph has to be acyclic there has to be at least one vertex that has no incoming edges, a so called source, our path has to start somewhere. This is then a possible start point for our topological order.
• Left to Right: The topological order is not unique, there can be multiple valid orders. But all of them have to follow the same pattern which can be seen in the example above. When the vertices are put in there topological order all the edges must go from left to right as all the vertices that depend on another vertex have to come after that vertex. If there was an edge going from right to left then the order would not be valid and there would be a cycle in the graph.

To find a topological order there are mainly two algorithms that are used that both make use of the fact that the graph must be acyclic and have a sink.

Example

Reverse-Post-Order of DFS

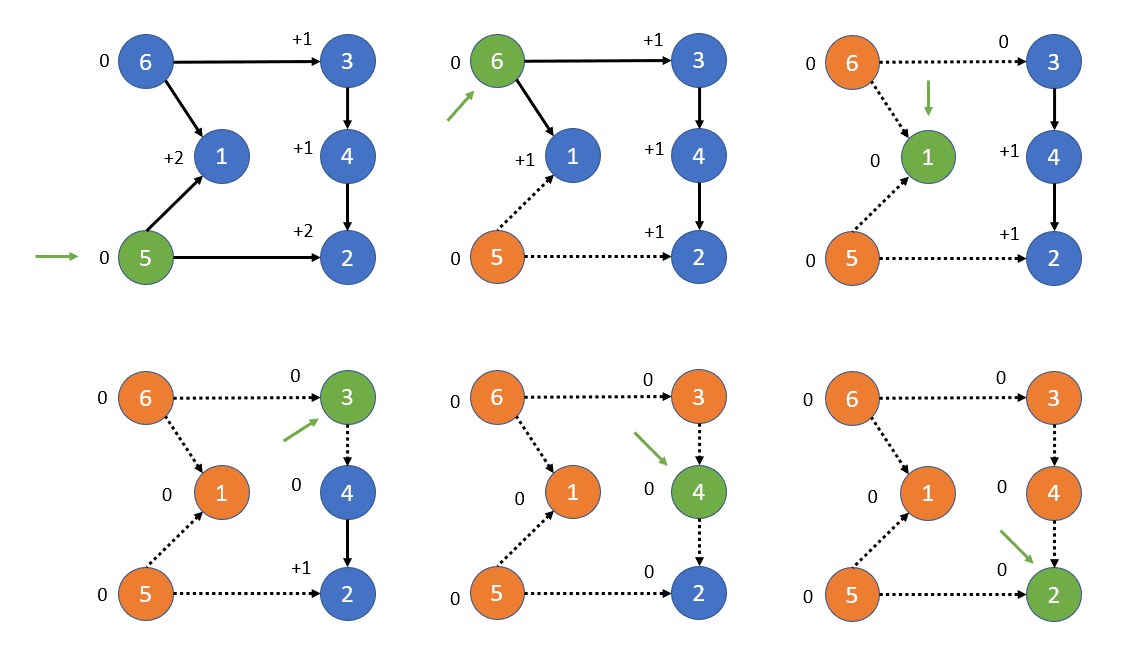
In the Depth First Search (DFS) section we have already seen that there we can come up with different orderings of the vertices depending on the order in which we visit them. One of these orderings post order which is the order in which the nodes are last visited. So the first node in the post order is the deepest node in the tree that we reach with the first recursive calls before we backtrack. From this node we can not go any further So it must be a sink in the graph or a neighbour to an already visited node which would form a cycle and therfore the graph would not have a topological order. Because it is a sink it must be one of the last nodes in the topological order (not guaranteed to be the last node as there can be multiple sinks). If we continue this process we actually notice that the reverse of the post order is a valid topological order. So we can use the DFS algorithm to find a topological order in \(O(|V|+|E|)\) time. Again we can use the adjacency list to make the algorithm more efficient. It can also be implemented using a stack rather than recursion but the idea is the same and the code just gets a bit more complicated.

public List<Integer> topologicalOrder(List<List<Integer>> graph, int start) {
    boolean[] visited = new boolean[graph.size()];
    List<Integer> order = new ArrayList<>();
    dfs(graph, start, visited, order);
    
    // if the has a cycle or is not connected
    if (order.size() != graph.size()) {
        return Collections.emptyList();
    }
 
    Collections.reverse(order);
    return order;
}
 
private void dfs(List<List<Integer>> graph, int node, boolean[] visited, List<Integer> order) {
    visited[node] = true;
    for (int neighbor : graph.get(node)) {
        if (!visited[neighbor]) {
            dfs(graph, neighbor, visited, order);
        } else {
            // we found a cycle
            order.clear();
        }
    }
    order.add(node);
}

Kahn’s Algorithm

Kahns algorithm makes use of the fact that sinks have no vertices that depend on them. So we can start by finding all the sinks in the graph and add them a list. Then we remove the first sink from the list and add it to our topological order. We then remove all the edges that lead to the sink. If by removing the edges we find a new sink we add it to the list. We continue this process until there are no vertices left in the graph. If there are still vertices left in the graph then there is a cycle in the graph and there is no topological order. The time complexity of Kahns algorithm is \(O(|V|+|E|)\) as we have to go through all the vertices and edges at least once. You can also implement this algorithm by starting at a source and removing the edges and then going to the next source and so on.

public List<Integer> topologicalOrder(List<List<Integer>> graph) {
    int[] inDegree = new int[graph.size()];
    for (List<Integer> neighbors : graph) {
        for (int neighbor : neighbors) {
            inDegree[neighbor]++;
        }
    }
 
    List<Integer> order = new ArrayList<>();
    Queue<Integer> queue = new LinkedList<>();
    for (int i = 0; i < inDegree.length; i++) {
        if (inDegree[i] == 0) {
            queue.enqueue(i);
        }
    }
 
    while (!queue.isEmpty()) {
        int node = queue.dequeue();
        order.add(node);
        for (int neighbor : graph.get(node)) {
            inDegree[neighbor]--;
            if (inDegree[neighbor] == 0) {
                queue.enqueue(neighbor);
            }
        }
    }
 
    if (order.size() != graph.size()) {
        return Collections.emptyList();
    }
 
    return order;
}