Depth First Search

The depth first search (DFS) algorithm is along with breadth first search (BFS), one of the most widely used algorithms in graph theory. Both of these algorithms are used to traverse a graph, so starting at a given vertex, they visit all the vertices in the graph. The difference between the two algorithms is the order in which they visit the vertices.

Whilst BFS explores the graph by visiting all the vertices at the present level before moving on to the next level, so it goes as wide as possible before going one level deeper, hence the name breadth first search, DFS explores the graph by following a path as deep as it can go and then backtracking to a node with unexplored neighbors, hence the name depth first search.

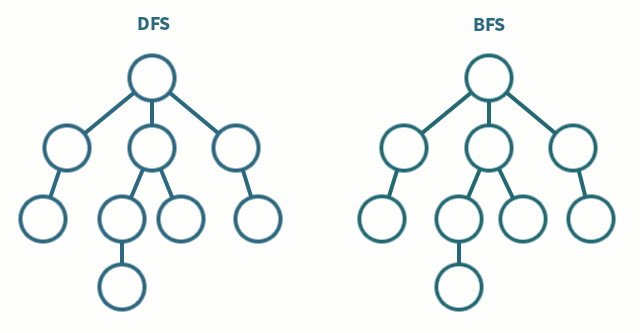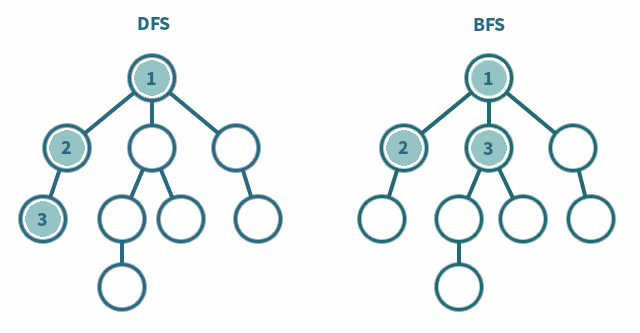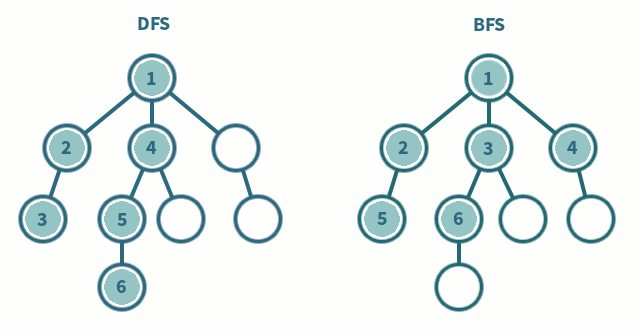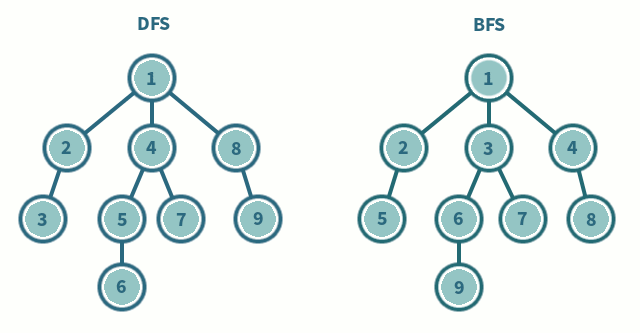
DFS is easiest to implement using recursion. The idea is to start at a node mark it as visited and then recursively call the DFS function on all of its neighbors that have not been visited yet. Once we reach a node that has no unvisited neighbors, we backtrack to the previous node and continue the process. The DFS functions is called on all nodes onces so \(n\) times and the for loop to check the neighbors runs \(n\) times as well due to the adjacency matrix representation of the graph. Hence, the time complexity of DFS is \(O(n^2)\).

public void dfs(boolean[][] graph, int start) {
    boolean[] visited = new boolean[graph.length];
    dfs(graph, start, visited);
}
 
private void dfs(boolean[][] graph, int node, boolean[] visited) {
    visited[node] = true;
    System.out.println(node);
    for (int i = 0; i < graph.length; i++) {
        if (graph[node][i] && !visited[i]) {
            dfs(graph, i, visited);
        }
    }
}

However, if we use an adjacency list representation of the graph, the time complexity of DFS is \(O(n+m)\), where \(n\) is the number of nodes and \(m\) is the number of edges. As the work in the inner loop becomes \(1 + d(v)\), where the one operation is to mark the node as visited and \(d(v)\) is the degree of the node \(v\). Hence, the time complexity of DFS becomes \(O(n+m)\).

public void dfs(List<List<Integer>> graph, int start) {
    boolean[] visited = new boolean[graph.size()];
    dfs(graph, start, visited);
}
 
private void dfs(List<List<Integer>> graph, int node, boolean[] visited) {
    visited[node] = true;
    System.out.println(node);
    for (int neighbor : graph.get(node)) {
        if (!visited[neighbor]) {
            dfs(graph, neighbor, visited);
        }
    }
}

Because of the recursive nature of the DFS algorithm we can visualize the algorithm as a tree, the so called DFS tree. The tree is rooted at the starting node and the children of a node are the nodes that are visited from the recursive call on that node. The edges in the tree are the edges in the original graph that are traversed by the DFS algorithm.

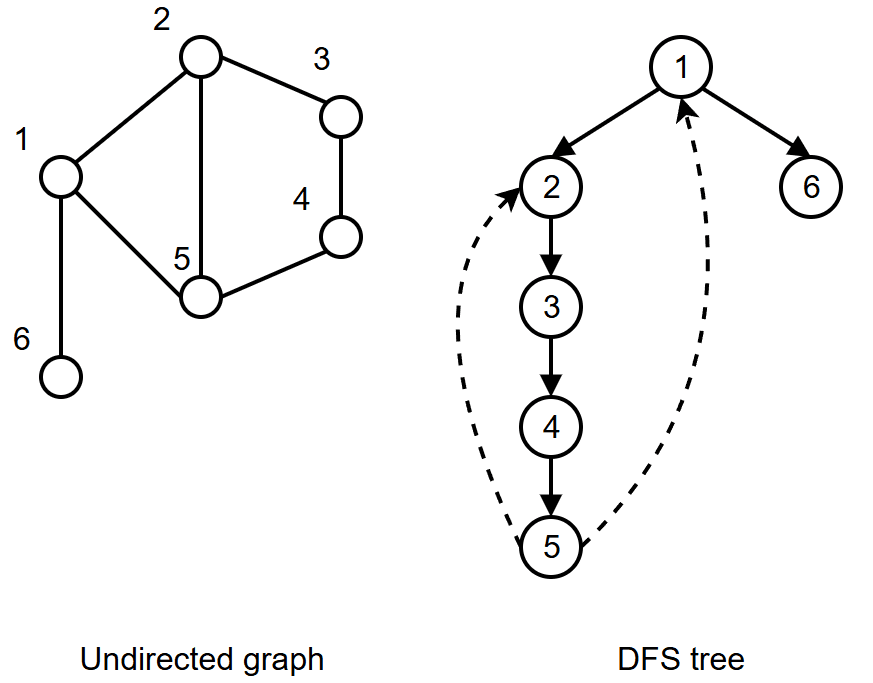
To avoid the potential stack overflow when using recursion on large graphs, we can use an explicit stack to implement DFS iteratively. The idea is to push the starting node onto the stack and mark it as visited. We then enter a loop where we pop a node from the stack and push all its unvisited neighbors onto the stack and mark them as visited. So rather then using the call stack to keep track of the nodes, we use an explicit stack. The time complexity of the iterative implementation of DFS is the same as the recursive implementation, \(O(n+m)\).

public void dfs(List<List<Integer>> graph, int start) {
    boolean[] visited = new boolean[graph.size()];
    Stack<Integer> stack = new Stack<>();
    stack.push(start);
    visited[start] = true;
    while (!stack.isEmpty()) {
        int node = stack.pop();
        System.out.println(node);
        for (int neighbor : graph.get(node)) {
            if (!visited[neighbor]) {
                stack.push(neighbor);
                visited[neighbor] = true;
            }
        }
    }
}

Applications of Depth First Search (DFS) include:

• Finding cycles or bridges
• Topological Sorting
• Finding strongly connected components

Orderings

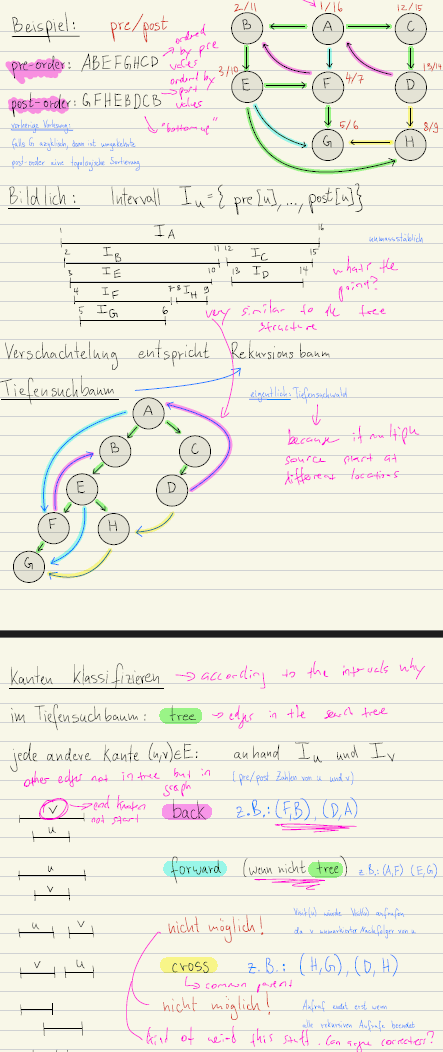
If we keep track of the time when a node is first visited and the time when we have last visited a node when backtracking, we can create different orderings of the nodes in the graph.

public void dfs(List<List<Integer>> graph, int start) {
    boolean[] visited = new boolean[graph.size()];
    int time = 0;
    int[] pre = new int[graph.size()];
    int[] post = new int[graph.size()];
    dfs(graph, start, visited, time, pre, post);
}
 
private void dfs(List<List<Integer>> graph, int node, boolean[] visited, int time, int[] pre, int[] post) {
    visited[node] = true;
    pre[node] = time++;
    for (int neighbor : graph.get(node)) {
        if (!visited[neighbor]) {
            dfs(graph, neighbor, visited, time, pre, post);
        }
    }
    post[node] = time++;
}

This results in three different orderings of the nodes in the graph:

• Pre-ordering: The order in which the nodes are first visited. Which is the order in which the nodes are “discovered” and for me the most intuitive ordering.
• Post-ordering: The order in which the nodes are last visited. It turns out that the post-ordering is the reverse of the topological ordering of the graph if the graph is a directed acyclic graph (DAG).
• In-ordering: The order in which the nodes are visited when backtracking. This only works if the graph is a tree as otherwise the order is not unique due to backtracking multiple times to the same node.

Back, Forward and Cross Edges

When traversing a graph using DFS, we build up the DFS tree. The edges we take to traverse the graph are the ones that are in the DFS tree and are therefore called tree edges. For all the other edges in the graph, we can classify them into three categories by either adding them to the DFS tree or by analysing the intervals of each node that is spanned by the pre and post times.

• Back Edges: An edge \((u, v)\) is a back edge if \(v\) is an ancestor of \(u\) in the DFS tree. This means that the there is a cycle in the graph because there is a path down the tree somehow from \(v\) to \(u\) and then there is a way back up the tree from \(u\) to \(v\).
• Forward Edges: An edge \((u, v)\) is a forward edge if \(v\) is a descendant of \(u\) in the DFS tree but \((u, v)\) is not a tree edge. This means that there is a more direct path from \(v\) to \(u\) then the path down the tree.
• Cross Edges: An edge \((u, v)\) is a cross edge if \(u\) and \(v\) are not in each others subtree. This means that the edge connects two different branches of the DFS tree.

Tarjan’s Bridge Finding Algorithm

As mentioned above if we know there is a back edge in the graph, we know there is a cycle in the graph. There is a similar property for forward edges, which can be thought of as another path or shortcut between two nodes. This is what Tarjan’s bridge finding algorithm exploits to find bridges in a graph. A bridge is an edge in a graph that if removed would increase the number of connected components in the graph, hence it is also often called a critical or cut edge.

Finding Strongly Connected Components

Sounds very similar to finding bridges, but the idea is to find groups of nodes that are connected to each other in a directed graph.