Searching

The idea of searching algorithms is to find a specific item in a collection of items. For example, given an array of integers, to the index of a specific integer. Depending on the application the items might have some structure or ordering. In the case of an array of integers, they might be sorted ascending/descending (structured) or unsorted (unstructured). We can define the task of searching as follows:

Given a collection \(A\) of \(n\) items and a target item \(x\), find the index \(i\) such that \(A[i] = x\). If \(x\) is not in \(A\), return \(-1\).

A potential real-world analogy would be if you were given a collection of playing cards and asked to find the Queen of Hearts.

Linear Search

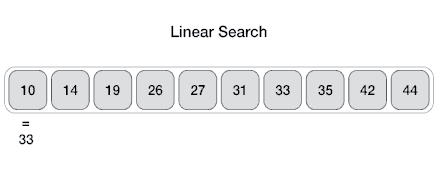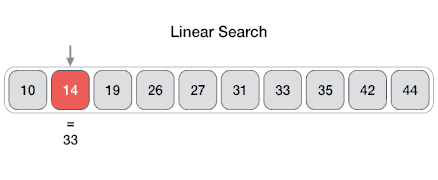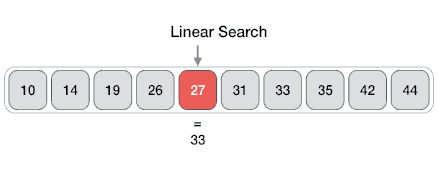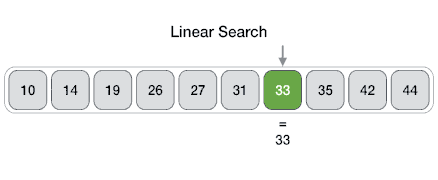
The most intuitive approach for most people to finding an item in a collection that is unstructured, i.e. not sorted, is the linear would be to start at the beginning and check each item one by one until the target item is found.

public int linearSearch(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

Correctness

The correctness of the linear search algorithm is quite obvious. If the target item is in the collection, we will eventually find it. If the target item is not in the collection, we will check every item and return \(-1\).

Analysis

To analyze the time complexity of the linear search algorithm, we focus on the number of comparisons that we have to make.

In the worst-case scenario, the target item is not in the collection, and we have to check every item. This results in a time complexity of \(O(n)\). This is also what gives it the name “linear search” as the time complexity grows linearly with the size of the collection, \(n\). Sometimes the linear search is also called the sequential search as it searches the collection sequentially, one item at a time.

In the best case scenario, the target item is the first item in the collection, and we only have to check one item. This results in a time complexity of \(\Omega(1)\).

We can also analyze the time complexity formally using a recurrence relation:

where \(c\) is the time it takes to check if the target item is equal to the current item. We can quickly come to the hypothesis via for example telescoping that \(T(n) \leq n \cdot c\) and prove with induction that the time complexity of the linear search algorithm really is \(O(n)\).

Lower Bound of Unstructured Search

Is linear search the most optimal algorithm using comparisons that we can use to search an unstructured collection? Importantly here we as always in computer science are interested in the worst-case scenario. So can we do better than \(O(n)\) comparisons in the worst-case scenario?

The answer is yes. The lower bound of unstructured search is therefore \(\Omega(n)\) which also means that the linear search is optimal for unstructured collections and in \(\Theta(n)\).

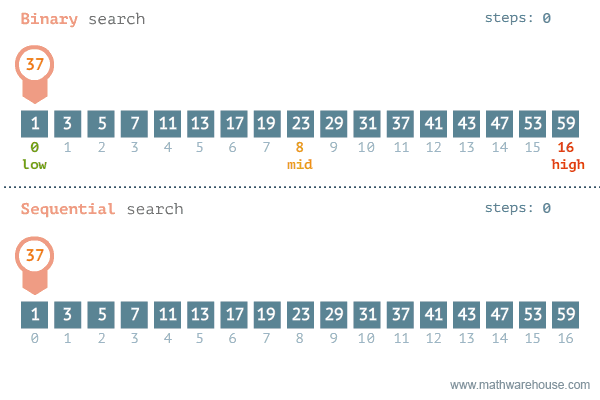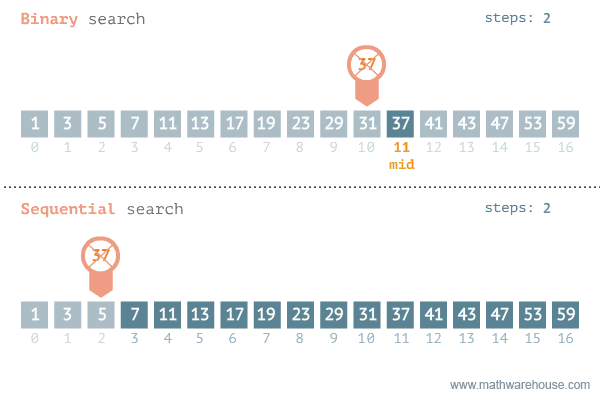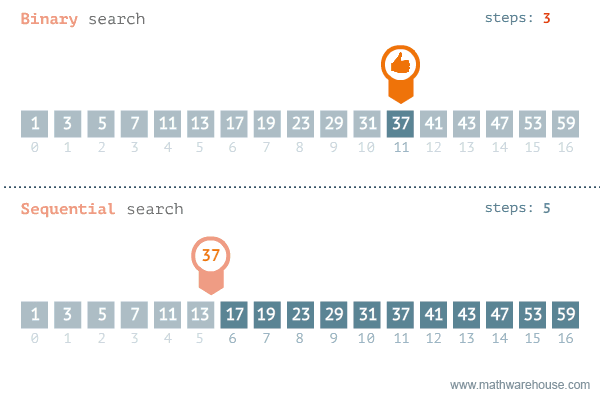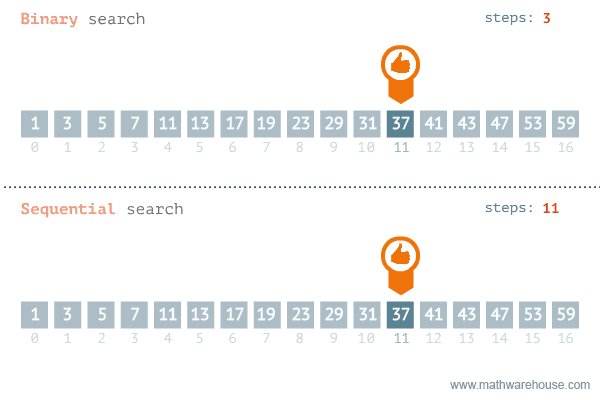
Binary Search

If the collection is structured, i.e. sorted, we can use a more efficient algorithm called binary search. More formally we can say that a collection of \(n\) integers is sorted if the following holds:

The idea of binary search is a divide and conquer approach. We start by comparing the target item with the middle item of the collection:

1. If the target item is equal to the middle item, we have found the target.
2. If the target item is less than the middle item, we know that the target item must be in the left half of the collection, due to the collection being sorted.
3. If the target item is greater than the middle item, we know that the target item must be in the right half of the collection. We then repeat the process on the half of the collection where the target item must be until we find the target item or we run out of items to check.

public int binarySearch(int[] arr, int target) {
    int low = 0;
    int high = arr.length - 1;
    while (low <= high) {
        int mid = low + (high - low) / 2;
        if (arr[mid] == target) {
            return mid; // target found
        } else if (arr[mid] < target) {
            low = mid + 1; // target is in the right half
        } else {
            high = mid - 1; // target is in the left half
        }
    }
    return -1;
}

Correctness

The correctness of the binary search algorithm is also quite obvious. If the target item is in the collection, we will eventually find it by dividing the collection in half each time. If the target item is not in the collection, we will eventually run out of items to check.

Analysis

To analyze the time complexity of the binary search algorithm, we can use a recurrence relation. We avoid having issues with rounding and splitting the collection by assuming that the collection size is a power of 2. So we let \(n = 2^k\) where \(k\) is the number of times we can divide the collection in half. By analyzing the algorithm we get the following recurrence relation:

where \(c\) is the time it takes to check a collection of size 1 and \(d\) is the time it takes to check and divide the collection. By telescoping the recurrence relation, the master theorem or trying out some examples, we come across the hypothesis that \(T(n) \leq \log(n) \cdot d + c\) for \(n = 2^k\) and \(k \leq 0\), making the time complexity of the binary search algorithm \(O(\log(n))\).

Lower Bound of Structured Search

Just like with unstructured search, we also want to know if the binary search algorithm is the most optimal algorithm using comparisons that we can use to search a structured collection.

The answer is yes. The lower bound of structured search is \(\Omega(\log(n))\) which also means that the binary search is optimal for structured collections and in \(\Theta(\log(n))\). To prove this, we use an argument from information theory that is based on a decision tree model.

Proof

The idea of the proof is simple. We design a decision tree where each node represents a comparison, so it can be either true or false. This makes the decision tree a binary tree. With each comparison, we reduce the number of items that we have to check and each leaf node represents a possible outcome of the search. So a search can be seen as taking a path from the root to a leaf node, where the leaf node represents the search outcome. Because there are \(n\) items in the collection, and they are all possible outcome, and we also have to account for the possibility that the target item is not in the collection, we have to have \(n+1\) leaf nodes in the decision tree. Therefore the height of the decision tree represents the worst-case number of comparisons that we have to make to find the target item. A binary tree with a single node has a height of 0, with a height of 1 it has at most 2 leaf nodes, with a height of 2 it has at most 4 leaf nodes, and so on. So with a height of \(h\), the decision tree has at most \(2^h\) leaf nodes. Therefore the decision tree needs to satisfy the following inequality:

\[n + 1 \text{outcomes} \leq \text{number of leaf nodes} \leq 2^h \]

By solving the inequality, we get that the height of the decision tree and therefore the number of comparisons that we have to make is at least \(\log(n+1)\), proving that the lower bound of structured search is \(\Omega(\log(n+1)) = \Omega(\log(n))\).

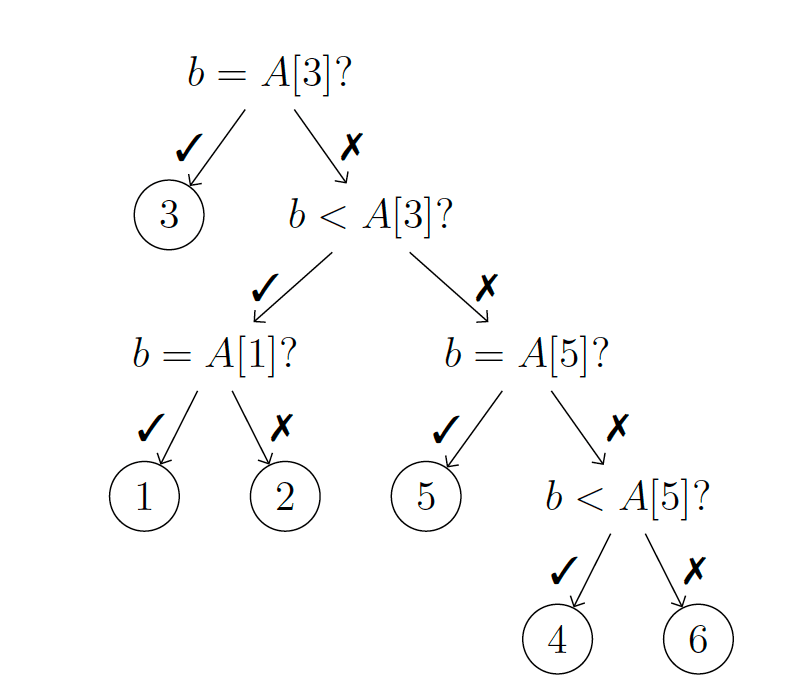
Inserting into a Sorted Array

Binary search can also be used to find the correct position to insert an item into a sorted array.

Interpolation Search

improvement over Binary Search for instances, where the values in a sorted array are uniformly distributed

Exponential Search

Same as Jump Search?