Maximum Segment Sum

The maximum segment sum problem or also known as the maximum subarray sum problem is a classic problem that can be solved using dynamic programming. The problem is to find the maximum sum of a contiguous subarray or segment of an array of integers. So we are given an array of integers that can be both positive and negative and we need to find the segment and its sum that has the maximum sum.

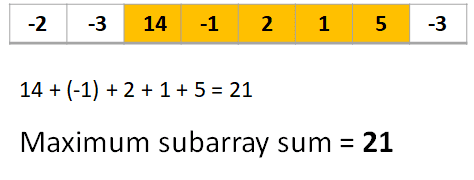
An example scenario of where this problem can be applied is in the stock market. You are given the hourly difference between the current and the opening price which would lead to having both positive and negative values. The problem is to find the segment of time where you should buy and sell the stock to maximize your profit. If the values are all negative then the maximum segment sum would be 0 as you would not buy the stock, this doesn’t quiet make sense in the stock market but it is a valid solution to the problem. If the values are all positive then the maximum segment sum would be the sum of all the values as you would buy the stock at the beginning and sell it at the end.

We can also write this a bit more formally. We are given an array of integers \(A\) of length \(n\) so \(A = [a_1, a_2, \ldots, a_n]\). We need to find the maximum segment sum defined as follows:

Brute Force

Unless you initially know that the problem can be solved with DP the most common first approach would be to just calculate the sum of all possible segments and keep track of the maximum sum. This approach has a time complexity of \(O(n^3)\).

int maxSegmentSum(int[] A) {
    int n = A.length;
    int maxSum = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            int sum = 0;
            for (int k = i; k <= j; k++) {
                sum += A[k];
            }
            maxSum = Math.max(maxSum, sum);
        }
    }
    return maxSum;
}

How do we get to the time complexity of \(O(n^3)\)? If we think about it we are taking all possible combinations of \(i\) and \(j\) where \(i \leq j\) and then we are summing up all the elements in between. So for the segment \(S_{i,i}\) we have 1 addition, for \(S_{i,i+1}\) we have 2 additions, for \(S_{i,j}\) we have \(j-i+1\) additions. So if we have a fixed \(i\) and we want to count the number of additions for all possible \(j\) with gaussian sums we get:

We can quickly define a rough upper and lower bound for the above number as follows:

Now we can sum up all the additions for all possible \(i\) which corresponds to the outer loop in the code and our final result:

As we can see the time complexities are \(\Omega(n^3)\) and \(O(n^3)\) which means that the time complexity of the brute force solution is \(\Theta(n^3)\). So this solution is already polynomial which is good but we can do better. However we are calculating certain segments multiple times which is a waste of time. So we can already see that we can improve the time complexity by using memoization and only calculating the sum of each segment once. So instead we can make use of the fact that building up the sum of a segment can be done iteratively by storing the sum of the previous segment and adding the next element. So a very simple kind of memoization as follows which has a time complexity of \(O(n^2)\):

int maxSegmentSum(int[] A) {
    int n = A.length;
    int maxSum = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int sum = 0;
        for (int j = i; j < n; j++) {
            sum += A[j];
            maxSum = Math.max(maxSum, sum);
        }
    }
    return maxSum;
}

The derivation of this time complexity is a lot simpler as it comes down to the following sum that can be calculated with gaussian sums as well:

Divide and Conquer

Do actually have to calculate the sum of all segments, can some be skipped? We saw that with the merge sort algorithm we could get a time complexity of \(O(n \log n)\) using a divide and conquer approach. Maybe we can apply the same idea here.

If we think about the problem we can see that the maximum segment sum can be in the left half, the right half or it can be a segment that crosses the midpoint. So we can divide the problem into three subproblems and then recursively solve them. The base case would be when we have a segment of length 1 where the maximum segment sum is just the value of the element. So we can define the maximum segment sum as follows:

1. Solve the left and right subproblems recursively.
2. Find the maximum segment sum that crosses the midpoint.
3. Return the maximum of the three.

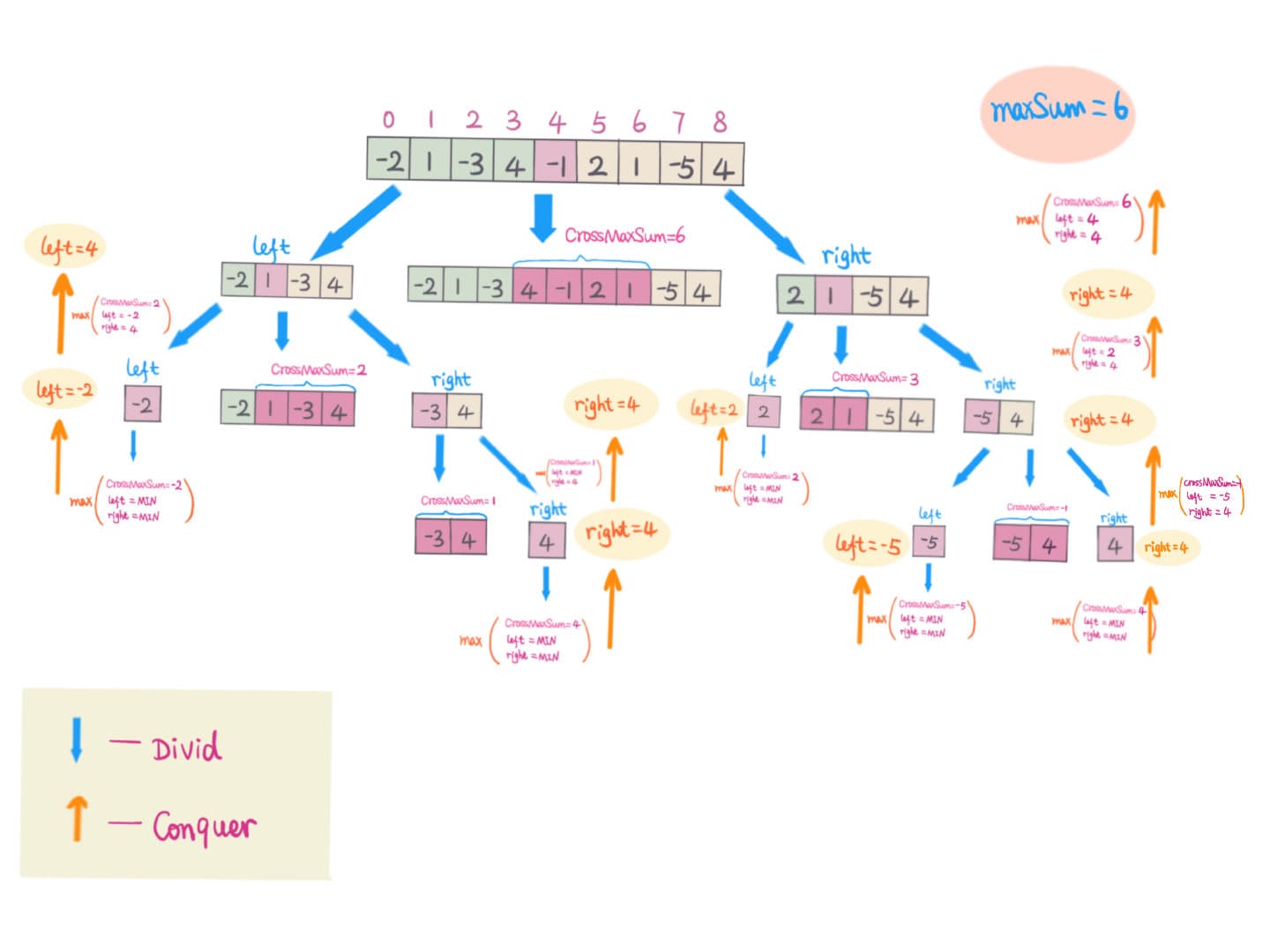
Finding the maximum segment sum that crosses the midpoint can be done by starting from the midpoint and going to the left and right. So we are actually finding the two maximum segment sums that end and start at the midpoint. The maximum segment sum that crosses the midpoint is then the sum of the two maximum segment sums. So we are calculating the following:

For simplicity when calculating we assume that the array has length \(n = 2^k\) for some \(k\). If the array has a different length we can just pad it with zeros. The time complexity of the divide and conquer approach is \(O(n \log n)\).

int maxSegmentSum(int[] A) {
    return maxSegmentSum(A, 0, A.length - 1);
}
 
int maxSegmentSum(int[] A, int low, int high) {
    if (low == high) {
        return A[low];
    }
    int mid = low + (high - low) / 2;
    int leftMax = Integer.MIN_VALUE;
    int sum = 0;
    for (int i = mid; i >= low; i--) {
        sum += A[i];
        leftMax = Math.max(leftMax, sum);
    }
    int rightMax = Integer.MIN_VALUE;
    sum = 0;
    for (int i = mid + 1; i <= high; i++) {
        sum += A[i];
        rightMax = Math.max(rightMax, sum);
    }
    int crossMax = leftMax + rightMax;
    return Math.max(crossMax, Math.max(maxSegmentSum(A, low, mid), maxSegmentSum(A, mid + 1, high)));
}

The derivation of the time complexity comes from the fact that calculating the maximum segment sum that crosses the midpoint takes \(1+2(\frac{n}{2} - 1) = n-1\) additions. So the time complexity can be calculated using the master theorem on the following recurrence relation:

Dynamic Programming

From the divide and conquer approach we can see that we are calculating the maximum segment sum that crosses the midpoint multiple times. We might also get the idea from the way we calculate the crossing maximum segment sum by calculating the sum that ends in the middle that we could do the same thing in a similar way by creating a table where each entry represents the maximum segment sum that ends at that index. So we can define something like this:

This is known as kadane’s algorithm and it has a time complexity of \(O(n)\) as each entry in the table can be calculated by either taking the previous entry and adding the current element or just taking the current element. The maximum segment sum is then the maximum of all the entries in the table.

int maxSegmentSum(int[] A) {
    int n = A.length;
    edgeMax = new int[n];
    edgeMax[0] = A[0];
    int maxSum = edgeMax[0];
    for (int i = 1; i < n; i++) {
        edgeMax[i] = Math.max(edgeMax[i - 1] + A[i], A[i]);
        maxSum = Math.max(maxSum, edgeMax[i]);
    }
    return maxSum;
}

Here again we can optimize the space complexity by just using a single variable to store the previous entry in the table.

int maxSegmentSum(int[] A) {
    int n = A.length;
    int edgeMax = A[0];
    int maxSum = edgeMax;
    for (int i = 1; i < n; i++) {
        edgeMax = Math.max(edgeMax + A[i], A[i]);
        maxSum = Math.max(maxSum, edgeMax);
    }
    return maxSum;
}

We can also quickly come to the conclusion that the time complexity of \(O(n)\) is optimal as we have to look at each element in the array at least once. The space complexity of \(O(1)\) is also optimal as we only need a constant amount of space to store the previous entry in the table.