Breadth First Search

The breadth first search (BFS) algorithm is probably the simplest algorithm on graphs to understand and along with depth first search (DFS), is one of the most widely used algorithms in graph theory. Both of these algorithms are used to traverse a graph, so starting at a given vertex, they visit all the vertices in the graph. The difference between the two algorithms is the order in which they visit the vertices.

Whilst DFS explores the graph by following a path as deep as it can go, hence the name depth first search, BFS explores the graph by visiting all the vertices at the present level before moving on to the next level, so it goes as wide as possible before going one level deeper, hence the name breadth first search.

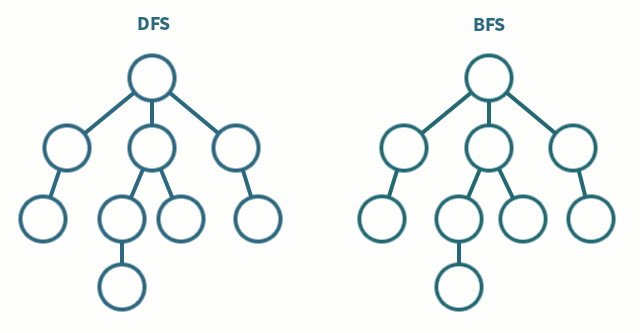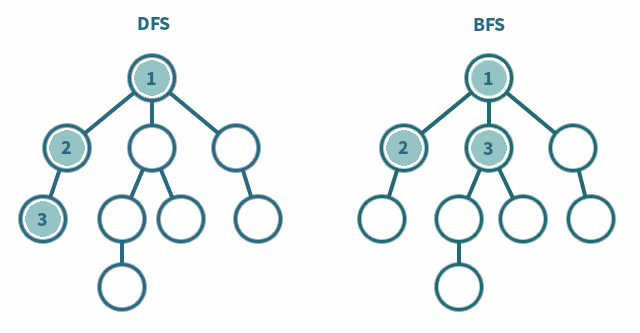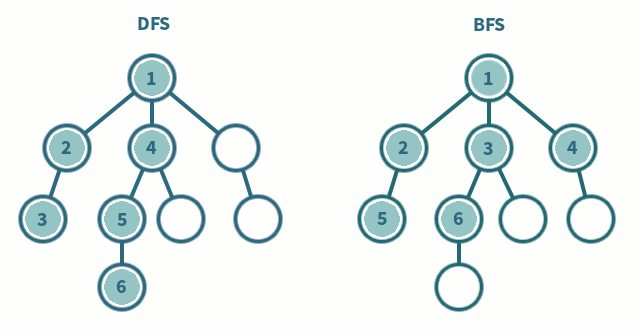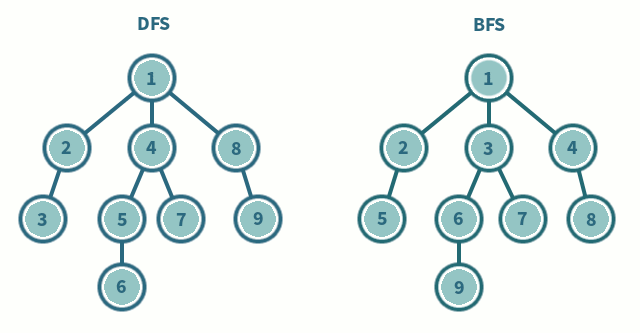
The idea of BFS is rather simple when implementing it with a queue. We add a starting node to the queue and mark it as visited. We then enter a loop where we dequeue a node from the queue and add all its unvisited neighbors to the queue and mark them as visited. We continue this process until the queue is empty. In the implementation below, the other loop runs \(n\) times as every node is only added to the queue once. Due to the adjacency matrix representation of the graph, the inner loop runs \(n\) times as well, as we have to check every node to see if it is a neighbor of the current node. Hence, the time complexity of BFS is \(O(n^2)\).

public void bfs(boolean[][] graph, int start) {
    boolean[] visited = new boolean[graph.length];
    Queue<Integer> queue = new LinkedList<>();
    queue.add(start);
    visited[start] = true;
    while (!queue.isEmpty()) {
        int node = queue.poll();
        System.out.println(node);
        for (int i = 0; i < graph.length; i++) {
            if (graph[node][i] && !visited[i]) {
                queue.add(i);
                visited[i] = true;
            }
        }
    }
}

However, if we use an adjacency list representation of the graph, the time complexity of BFS is \(O(n+m)\), where \(n\) is the number of nodes and \(m\) is the number of edges. So the work in the inner loop becomes \(1 + d(v)\) ,where the one operation is to mark the node as visited and \(d(v)\) is the degree of the node \(v\). Hence, the time complexity of BFS becomes \(O(n+m)\).

public void bfs(List<List<Integer>> graph, int start) {
    boolean[] visited = new boolean[graph.size()];
    Queue<Integer> queue = new LinkedList<>();
    queue.add(start);
    visited[start] = true;
    while (!queue.isEmpty()) {
        int node = queue.poll();
        System.out.println(node);
        for (int neighbor : graph.get(node)) {
            if (!visited[neighbor]) {
                queue.add(neighbor);
                visited[neighbor] = true;
            }
        }
    }
}

Applications of Breadth First Search (BFS) include:

• shortest path in unweighted graph or with equal weight
• Finding cycles in a graph
• Topological sorting
• Finding connected components in a undirected graph
• max flow with Ford-Fulkerson
• Testing bipartiteness