Longest Common Subsequence

The longest common subsequence (LCS) problem is one of the most common dynamic programming problems. It is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in bioinformatics for comparing DNA sequences. The problem is as follows:

Given two sequences, find the length of the longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous. For example, “abc”, “abg”, “bdf”, “aeg”, “acefg”, .. etc are subsequences of “abcdefg”.

So for example if the input sequences are \(A=\text{"TIGER"}\) and \(B=\text{"ZIEGE"}\), the longest common subsequence is “IGE” and its length is 3.

An initial idea would be to generate all subsequences of both strings and then find the longest common subsequence. However, this approach would have an exponential time complexity of \(O(2^n)\), where \(n\) is the length of the input strings. Instead, what if we though of solving a subproblem first such just looking at the first \(i\) characters of \(A\) and \(B\)?

So for the example above if \(i=4\) Then the subproblem would be to find the longest common subsequence of the first 4 characters of \(A\) and \(B\) which would be “IE” or “IG”. This is also where the problem with this idea lies as there are multiple possible subsequences of the same length we would have to remember them all as if we increase \(i\) to 5 the longest common subsequence would be “IGE” so if we just would’ve remembered “IE” we would have missed the correct answer.

Instead we adapt our idea slightly be creating a 2D DP table where \(dp[i][j]\) will store the length of the longest common subsequence of the first \(i\) characters of \(A\) and the first \(j\) characters of \(B\). This leads to us having three possible cases for each cell in the table:

• If \(A[i]=B[j]\) then we can extend the longest common subsequence by 1 by adding the character \(A[i]\) to the longest common subsequence so far. This means that \(dp[i][j]=dp[i-1][j-1]+1\). We might however not want to take this solution as we might have found a longer common subsequence earlier on so we also have to consider the other two cases.
• We can ignore the character \(A[i]\) and try to find the longest common subsequence of the first \(i-1\) characters of \(A\) and the first \(j\) characters of \(B\). This means that \(dp[i][j]=dp[i-1][j]\).
• We can ignore the character \(B[j]\) and try to find the longest common subsequence of the first \(i\) characters of \(A\) and the first \(j-1\) characters of \(B\). This means that \(dp[i][j]=dp[i][j-1]\).

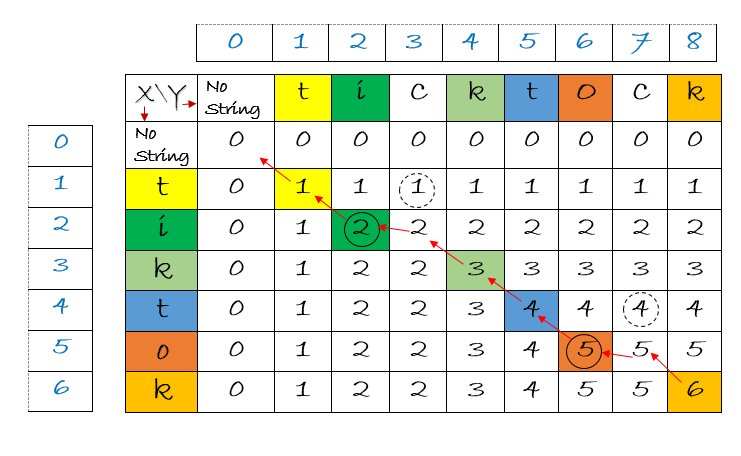
This leads to each entry in the table visually looking at the the left, top and top-left cell and taking the maximum of those three values and if \(A[i]=B[j]\) adding 1 to the top-left cell. The final answer will be stored in \(dp[m][n]\) where \(m\) and \(n\) are the lengths of \(A\) and \(B\) respectively.

public int longestCommonSubsequence(char[] A, char[] B) {
    int m = A.length;
    int n = B.length;
    int[][] dp = new int[m+1][n+1];
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (A[i-1] == B[j-1]) {
                // technically we can also look at the left and top cell values and pick the max but it is not necessary
                dp[i][j] = dp[i-1][j-1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }
        }
    }
    return dp[m][n];
}

The time complexity of this solution is \(O(mn)\) where \(m\) and \(n\) are the lengths of the input strings \(A\) and \(B\) respectively. The space complexity is also \(O(mn)\) as we are storing the entire DP table. However, this isn’t necessary as we only need the previous row to calculate the current row so we can reduce the space complexity to \(O(\min(m,n))\) by only storing the previous row and the current row.

There are better algorithms that do it in \(O((n+r) \log n)\) time where \(r\) is the number of matches between the two strings and \(n > m\).

Fixed Alphabet

If the alphabet of the input strings is fixed we can reduce the space complexity even further to \(O(n + m^2)\) where \(m\) is the shorter string so \(m \leq n\).