Heaps & Priority Queues
Simplify it to only hold unique keys.
We often want to be able to quickly extract the smallest or largest element from a collection. The most common first problem for this is when implementing the selection sort algorithm. In the selection sort we want to repeatedly want to find the smallest or largest element in the unsorted part of the array and move it to the correct position. The problem is that we have to search the whole array for the smallest or largest element which takes \(O(n)\) time and we have to do this \(n\) times which leads to a time complexity of \(O(n^2)\).
But what if we stored the elements in a way that finding the smallest or largest element would be faster? Obviously sorting the array would be a solution, but for our problem of improving the selection sort this doesn’t help. Instead we want a new data structure that allows us to find the smallest or largest element faster, such as in \(O(\log n)\) time. This is where heaps come in. Depending on whether we want to find the smallest or largest element we can more precisely define the data structure as a min-heap, where we can quickly find the smallest element, or a max-heap, where we can quickly find the largest element. We will be focusing on the max-heap in this article. Using a heap to implement the selection sort algorithm then leads to the heap sort algorithm which runs in \(O(n \log n)\) time.
For the heap we will use a binary tree where we enforce two properties:
- Completeness: We make sure that the tree stays complete, meaning that all levels are filled except for the last one, which is filled from left to right.
- Heap Property: We make sure that the key of each node is larger(smaller) than the keys of its children. This property is the key to finding the largest(smallest) element quickly as we can always find it in the root. Because the property is enforced for all nodes it means that either the left or right child of a node is the closest to the node.
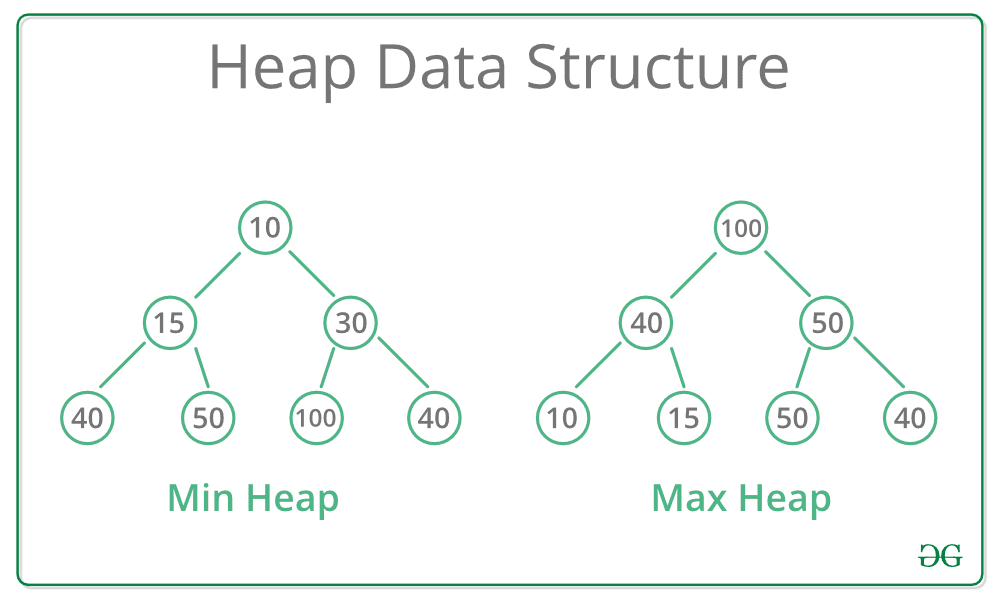
So we come to the conclusion that we will need 3 operations on our heap:
- Construct: We need to be able to construct a heap from an array of elements.
- Add: We need to be able to add an element to the heap. We also need to make sure that the heap property is maintained.
- Remove Root: We need to be able to remove the largest(smallest) element at the root of the heap. Here again we need to make sure that the heap property is maintained after the removal, which involves moving the new largest(smallest) element to the root.
Storing a Heap
Before we talk about how to perform operations on a heap we need to talk about how we can store a heap. The first way would be to use a linked node structure where each node has a reference to its parent and its children like a linked list. This however is not very efficient as we have to store a lot of references.
Instead what is most commonly used to store complete binary trees is an array. If we look at a binary tree we can quickly come up with an indexing scheme that allows us to find the parent, left child, and right child of a node.
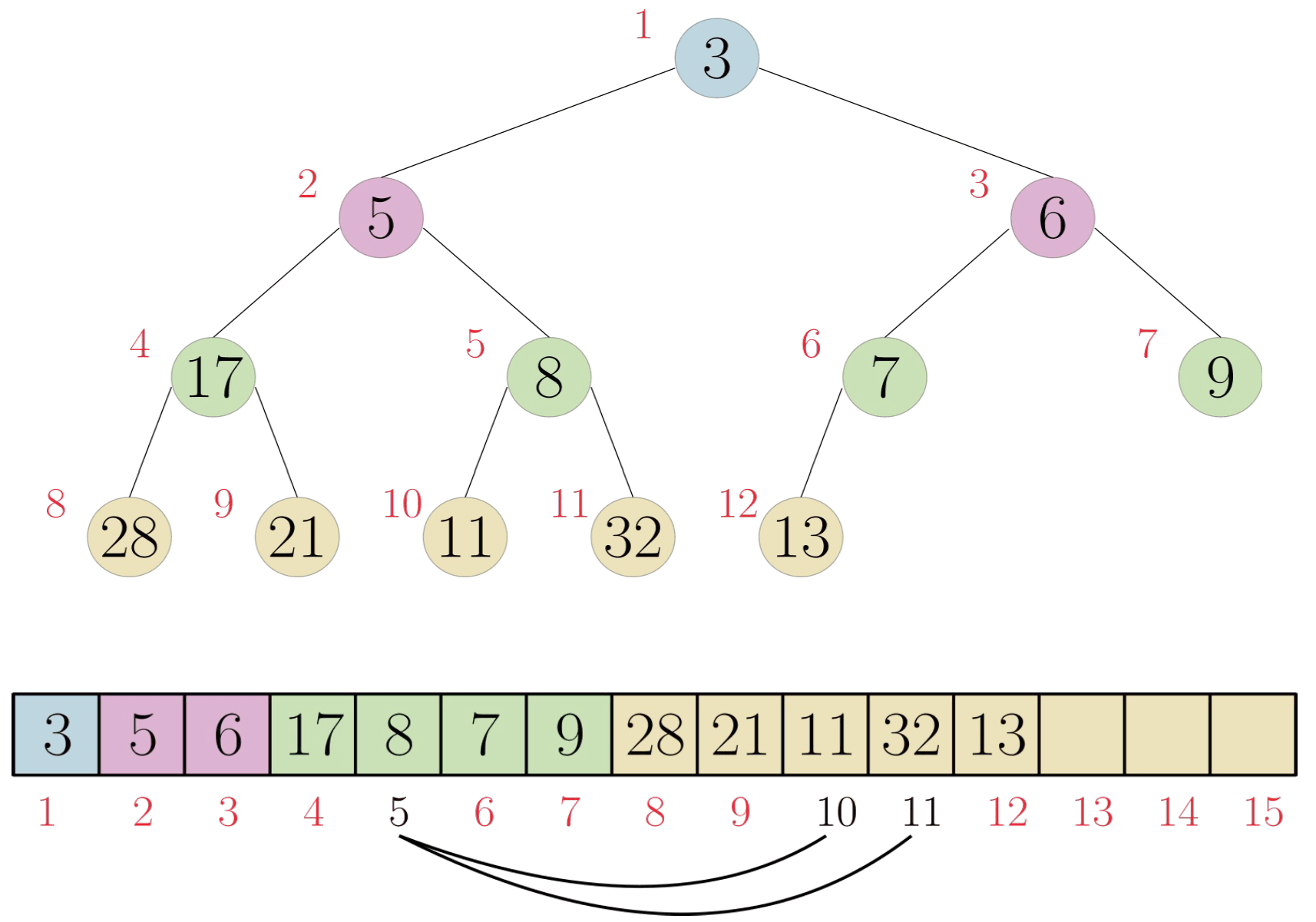
We place the root at index 1 and then for each node at index \(i\) we place its left child at \(2i\) and its right child at \(2i+1\). We can also reverse the calculation to find the parent of a node at index \(i\) by calculating \(\lfloor i/2 \rfloor\).
| Root at index 1 | |
|---|---|
| Left child of \(i\) | \(2i\) |
| Right child of \(i\) | \(2i+1\) |
| Parent Node of \(i\) | \(\lfloor i/2 \rfloor\) |
There is one problem with this indexing scheme and is also the largest drawback of heaps and why we don’t use the heap sort algorithm as much as other sorting algorithms. The problem is the lack of locality in the array. We are not accessing the elements in a contiguous way but rather jumping around the array. Making it harder for the CPU to cache the elements and slowing down the algorithm.
Remove Root
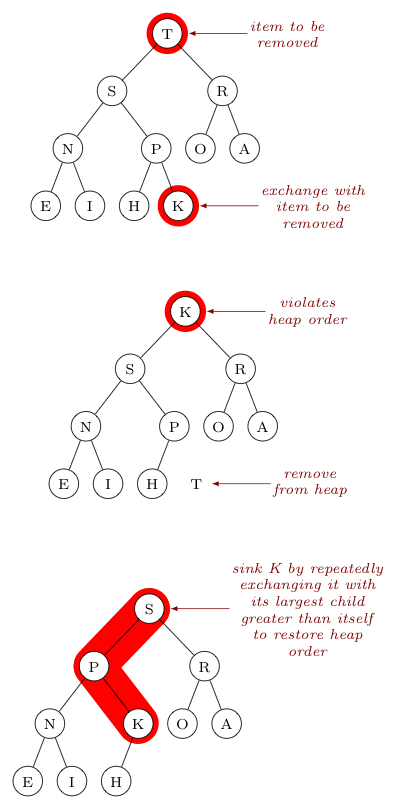
We know to extract the max or min element we can remove the root element. However doing so breaks the completeness property of the tree as it leaves a hole in the tree that needs to be filled. We fill this hole by taking the last element in the tree and placing it in the root. The last element is the rightmost element in the lowest level.
This restores the completeness property but the heap property will still be violated. To fix this we let the element “sift/sink down” the tree by swapping it with the larger of its children until it is larger than both its children or is a leaf. The name of the process comes from the fact that the element is slowly sinking down the tree. Because the tree has a height of \(O(\log n)\) and the element may have to sink down the whole height of the tree the time complexity of the sinking operation is \(O(\log n)\).
public class MaxHeap {
// root is at index 1
private int[] heap;
private int size;
public int removeRoot() {
int root = heap[1];
heap[1] = heap[size];
size--;
sinkDown(1);
return root;
}
private void sinkDown(int i) {
// while i has children
while (2 * i <= size) {
int j = 2 * i;
// find the larger child
if (j < size && heap[j] < heap[j + 1]) {
j++;
}
// heap property is satisfied
if (heap[i] >= heap[j]) {
break;
}
// swap
swap(i, j);
// move down the tree
i = j;
}
}
}Add
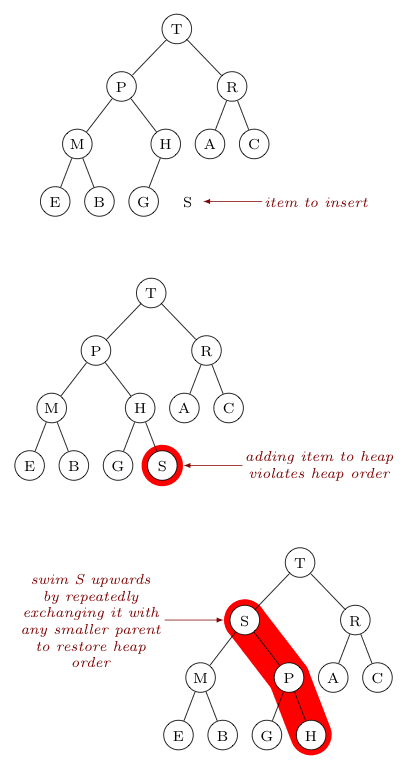
To add an element to the heap we first maintain the completeness property by adding the element to the next free spot in the tree. This will be the leftmost spot in the lowest level or the start of a new level. However most likely the heap property will be violated. To fix this we let the element “swim up” the tree by swapping it with its parent until it is smaller than its parent or is the root. Just like the sinking operation the swimming operation has a time complexity of \(O(\log n)\) as the tree has a height of \(O(\log n)\) and the element may have to swim up the whole height of the tree.
public class MaxHeap {
// root is at index 1
private int[] heap;
private int size;
public void add(int element) {
size++;
heap[size] = element;
swimUp(size);
}
private void swimUp(int i) {
// while i has a parent
while (i > 1) {
int j = i / 2;
// heap property is satisfied
if (heap[j] >= heap[i]) {
break;
}
// swap
swap(i, j);
// move up the tree
i = j;
}
}
}Constructing a Heap
With the above operations we know how to maintain the heap property when adding or removing elements. However, we first need to construct a heap from an array of elements to use these operations.
The most naive way to do this would be to add each element one by one to the heap using the add operation.
public class MaxHeap {
private int[] heap;
private int size;
public MaxHeap(int[] elements) {
heap = new int[elements.length + 1];
for (int i = 0; i < elements.length; i++) {
add(elements[i]);
}
}
}However this takes \(O(n \log n)\) time as adding an element to the heap takes \(O(\log n)\) time and we have to do this \(n\) times. You might think that because in the begging the heap is empty and the first elements don’t need to swim as far up the tree the time complexity would be less than \(O(n \log n)\) but this is not the case:
\[\begin{align*} T(n) &= \log 1 + \log 2 + \log 3 + \ldots + \log n \\ &= \sum_{i=1}^{n} \log i \\ &= \log(1 \cdot 2 \cdot 3 \cdot \ldots \cdot n) \\ &= \log(n!) \approx O(n \log n) \end{align*} \]This would still allow us to sort an array in \(O(n \log n)\) time using the heap sort algorithm. However there is a more efficient way to construct a heap from an array of elements.
Floyd’s Heap Construction
Floyd’s heap construction algorithm is more efficient way to construct a heap from an array of elements. Rather than adding each element one by one we first place all elements in the heap array to uphold the completeness property. Now we just need to make sure that the heap property is satisfied for all nodes.
If our tree then has \(n\) nodes it will have \((\log n)+1\) levels. We then iterate over all levels of the tree starting at the second lowest level and call the sink operation for each node on that level. This is the same as calling the sink operation on all inner nodes of the tree. So the first call will be for the parent of the last node. If it is smaller than one of its children it will sink down the tree. For this subtree the heap property is now satisfied. We then move across the level to the next parent and repeat the process until all subtrees starting at the second lowest level have the heap property satisfied. We then move up to the next level and repeat the process until we reach the root.
We can prove using induction and the following invariant that the algorithm correctly constructs a heap:
Invariant(i): After the \(i\)-th iteration the subtree rooted at the \(i\)-th node has the heap property satisfied.
public class MaxHeap {
private int[] heap;
private int size;
public MaxHeap(int[] elements) {
heap = new int[elements.length + 1];
size = elements.length;
for (int i = 0; i < elements.length; i++) {
heap[i + 1] = elements[i];
}
int lastParent = size / 2;
for (int i = lastParent; i >= 1; i--) {
sinkDown(i);
}
}
}The analysis of the time complexity of Floyd’s heap construction algorithm is rather complex. But it can be shown that the time complexity is \(O(n)\). It is explained here and will one day be added to this article. https://youtu.be/VkKmmwzfIG4?t=444
Priority Queues
by default the order of insertion is not maintained. Can this be demonstrated? So we cant garantee “stableness” if we want to we could add timestamp to the key and then use that if the keys are equal.