Linked Lists
This will be split into abstract data types and data structures. And then the actual implementations
When implementing collections with arrays we can encounter a few issues. An array uses a fixed given size which leads us to implementing algorithms that only work for that fixed amount. To solve this issue when adding elements we could also make an array that is one size larger, copy everything over and then add the new element. Another approach is when the array gets full we increase its size by either a fixed amount that could also change depending on how many times we have already increased the size. Meaning the array is either always full or we use to much space. In java the ArrayList is implemented in such a way. When the array is full it creates a new array that is 50% larger and copies everything over.
Another approach to dynamically growing and shrinking collections is to use linked lists. You can imagine a linked to be like a chain. It consists of nodes that have a value and a reference of the next node. The linked list itself then just needs a reference to the first node and can then make its way through the list. With this method the size of the collection is dynamic and we can easily add, remove, search and insert elements. The only limit being the amount of memory available.
public class Node<E> {
E value;
Node next;
}
public class LinkedList<E> {
int size;
Node head;
// operations
}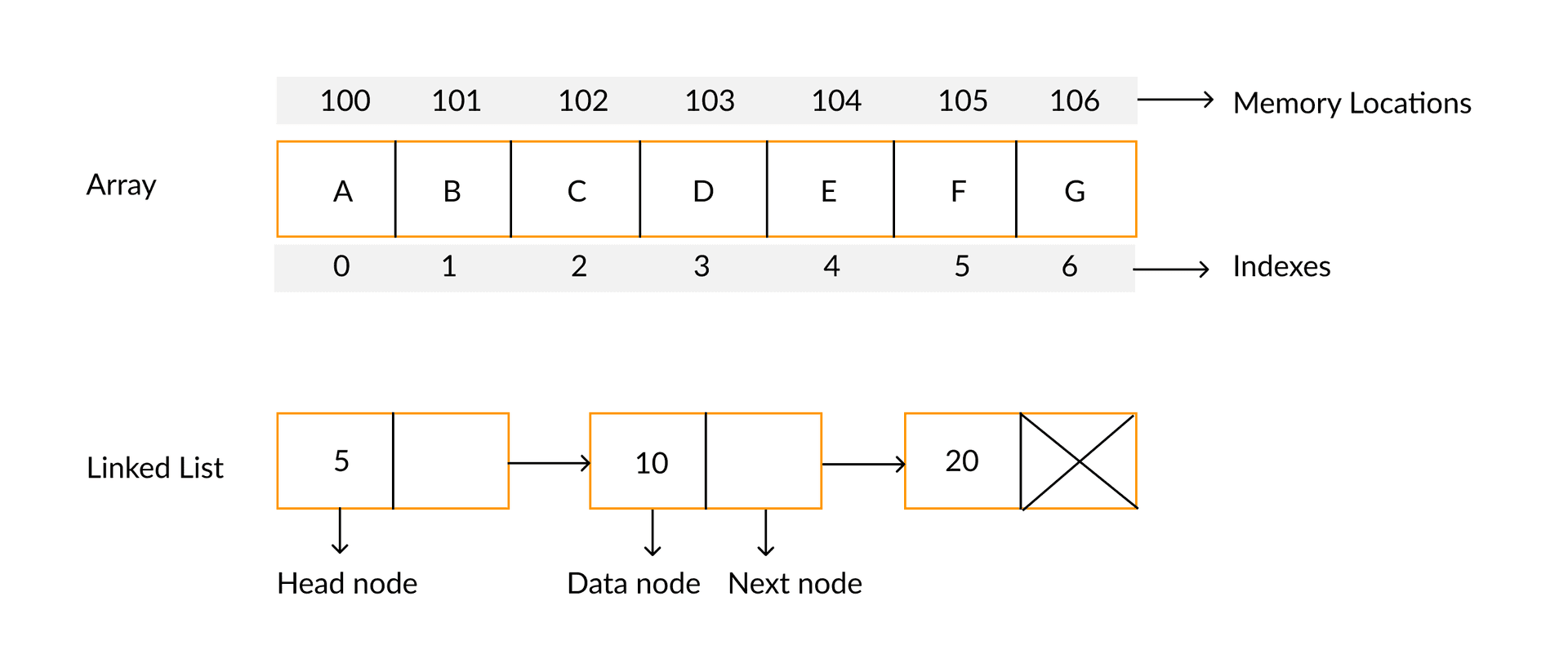
However, you might already see the drawback of linked lists. The use of references means that we need more memory to store the same amount of elements as in an array. Say for example in java a reference is 4 bytes and an integer is 4 bytes and we want to store 1000 integers. Then we have the following memory differences:
\[\text{Array} = 1000 \times 4 = 4000 \text{ bytes} \\ \text{Linked List} = 1000 \times (4 + 4) = 8000 \text{ bytes} \]This is not a precise calculation as there are also other factors to consider but it gives a good idea of the difference. There are also many different types of linked lists that have different memory costs but bring there own advantages and disadvantages when it comes to operations like adding, removing and searching elements.
Singly Linked List
The singly linked list is the most basic type of linked list. It is the one described above where each node has a value and a reference to the next node. The linked list itself then only needs a reference to the first node, the so called head. The last node, the so called tail, has no reference to the next node and instead references null.
There is also a double-ended linked list where the linked list also has a reference to the last node, the tail, in addition to the head. This makes adding elements to the end of the list much easier as you do not have to iterate through the entire list to find the last element. For example when implementing a queue you would use a double-ended linked list.
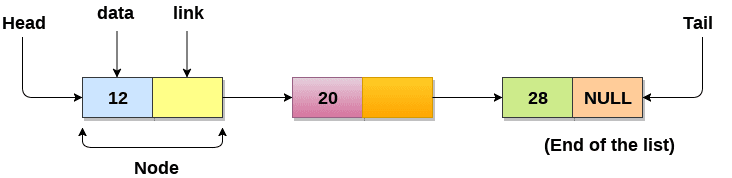
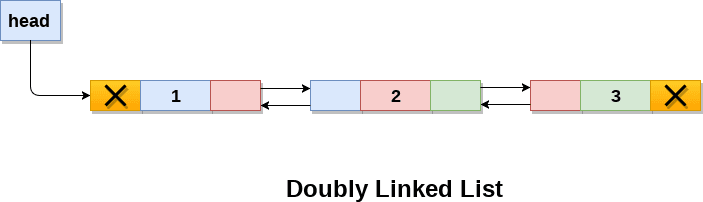
Doubly Linked List
The doubly linked list is an extension of the singly linked list where each node has in addition to the reference to the next node also a reference to the previous node. This can make operations like removing elements which you will see later how it can be done much easier.
Despite the image below the usual implementation of a doubly linked list is to have a reference to the head and the tail of the list. Meaning a double-ended doubly linked list doesn’t really exist.
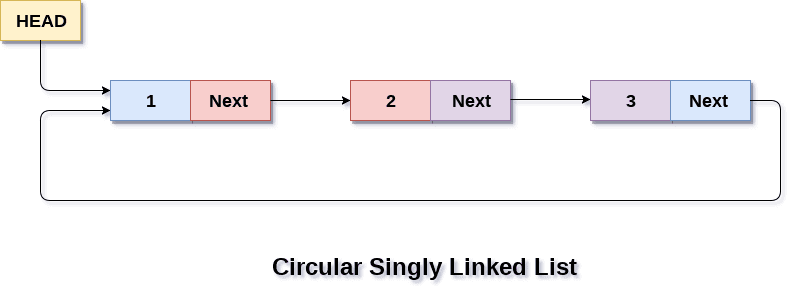
Circular Linked List
The circular linked list is again an extension of the singly linked list where the last element references the head again, forming a circle, rather than just null. This can also be done with a doubly linked list. However, I don’t really know of any use cases for a circular linked list at the moment of writing this.
Implementing a Linked List
When implementing a linked list the following operations are usually implemented:
- Adding & Inserting: We want to either add an element to the end of the list or insert it at a specific index or after a specific element.
- Removing: We want to remove an element from the list.
- Getting & Searching: We want to get an element at a specific index or search for a specific element.
A summary of the operations and their complexities can be found below:
| Type | Adding at end | Inserting at Index | Inserting after Element | Removing at Index | Removing Element | Getting at Index | Searching |
|---|---|---|---|---|---|---|---|
| Array | \(O(1)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) | \(O(1)\) | \(O(n)\) or \(O(\log n)\) |
| Singly Linked List | \(O(n)\) | \(O(n)\) | \(O(1)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| Double-ended Linked List | \(O(1)\) | \(O(n)\) | \(O(1)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) | \(O(n)\) |
| Doubly Linked List | \(O(1)\) | \(O(n)\) | \(O(1)\) | \(O(n)\) | \(O(1)\) | \(O(n)\) | \(O(n)\) |
Adding & Inserting
Depending on how we want to add or insert elements the complexity of the operation can vary. Lets start with just simply adding an element to the end of the list. For a normal singly linked list we have to iterate our way through the list to the end and then add the new element. This obviously has a complexity of \(O(n)\) which is not ideal for a simple operation.
public void add(E e) {
Node node = new Node(e);
// if the list is empty
if (head == null) {
head = node;
} else {
Node curr = head;
// iterate to the end of the list
while (curr.next != null) {
curr = curr.next;
}
curr.next = node;
}
size++;
}To solve the above issue we can use a double-ended linked list or a doubly linked list as they both have a reference to the tail. This way we can just add the new element to the end of the list without having to iterate through the entire list, making the operation \(O(1)\) and bringing it back to the same complexity as adding an element to the end of an array.
public void add(E e) {
Node node = new Node(e);
// if the list is empty
if (head == null) {
head = node;
tail = node;
} else {
tail.next = node;
tail = node;
}
size++;
}When we want to insert an element at a specific index we have no real choice but to iterate our way through the list to the index and then insert the new element. This has a complexity of \(O(n)\) which is no different from inserting an element at a specific index in an array as this also runs in \(O(n)\) as you have to shift all the elements after the index.
public void add(int index, E e) {
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException();
}
Node node = new Node(e);
// if the list is empty
if (head == null) {
head = node;
tail = node;
} else {
Node curr = head;
Node prev = null;
// iterate to the index
for (int i = 0; i < index; i++) {
prev = curr;
curr = curr.next;
}
// insert the new element
if (prev == null) {
node.next = head;
head = node;
} else {
prev.next = node;
node.next = curr;
}
}
size++;
}Lastly when we want to insert an element after a specific element we can actually gain an advantage over arrays. As we are given a reference to the element we want to insert after we can just set the reference of the new element to the reference of the element we want to insert after and then set the reference of the element we want to insert after to the new element. This has a complexity of \(O(1)\). In an array you would have to iterate your way through the array to find the element and then shift all the elements after the index.
public void addAfter(Node after, E e) {
Node node = new Node(e);
node.next = after.next;
after.next = node;
size++;
}Removing
We either want to remove an element at a specific index or remove a specific element. When removing an element at a specific index we have to iterate our way through the list to the index and then remove the element. This has a complexity of \(O(n)\) which is the same as removing an element at a specific index in an array due to the shifting of elements.
The process of removing works again with the analogy of a chain. When iterating through the list we have to keep track of the previous node to the current node. So we can “break” the chain and then “reconnect” it.
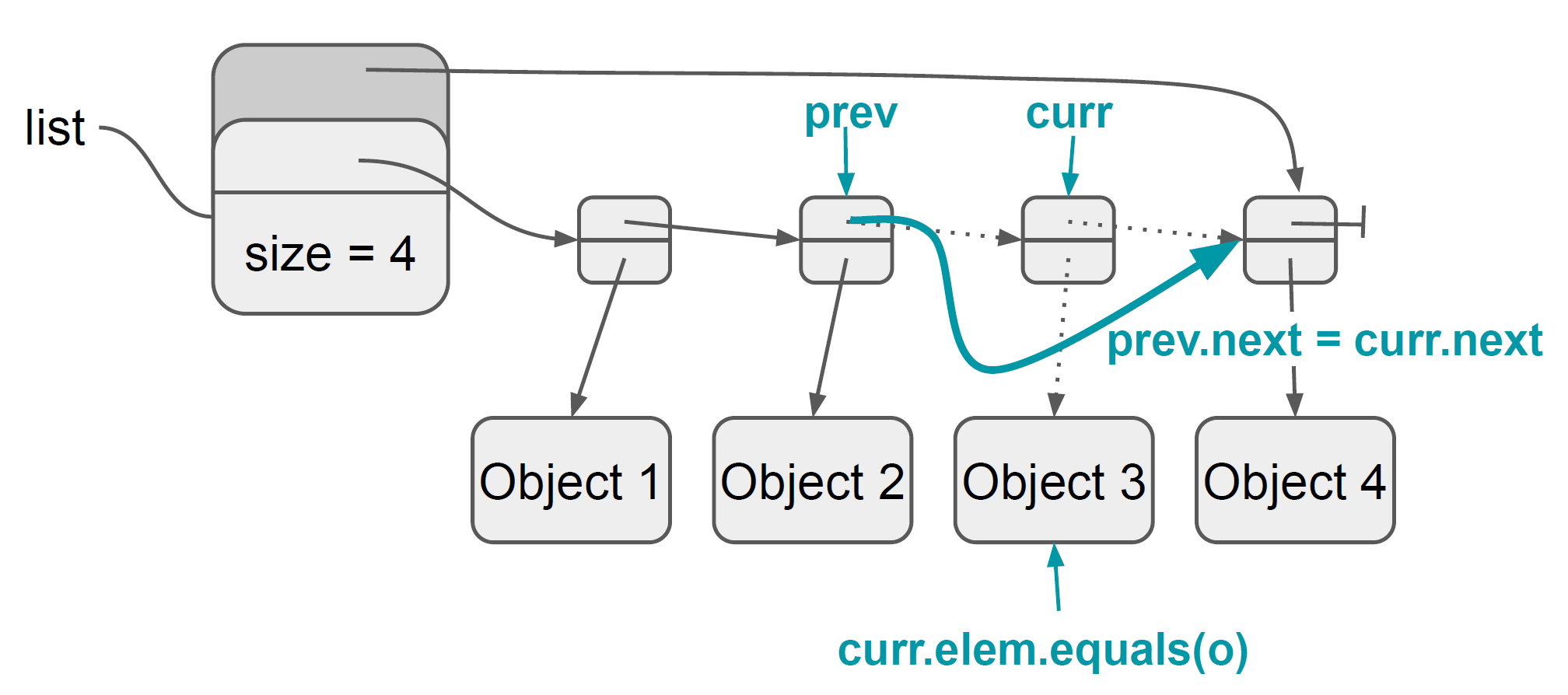
public void remove(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
// if the list is empty
if (head == null) {
return;
}
// if the element is the head
if (index == 0) {
head = head.next;
} else {
Node curr = head;
Node prev = null;
// iterate to the index
for (int i = 0; i < index; i++) {
prev = curr;
curr = curr.next;
}
// remove the element
prev.next = curr.next;
if (curr == tail) {
tail = prev;
}
}
size--;
}If we want to remove a specific element we have to iterate our way through the list to the element and then remove it. The same goes for removing an element from an array but with the added complexity of having to shift all the elements after the index. This has a complexity of \(O(n)\).
public void remove(E e) {
// if the list is empty
if (head == null) {
return;
}
// if the element is the head
if (head.value.equals(e)) {
head = head.next;
size--;
return;
}
Node curr = head;
Node prev = null;
// iterate to the element
while (curr != null && !curr.value.equals(e)) {
prev = curr;
curr = curr.next;
}
// remove the element
if (curr != null) {
prev.next = curr.next;
if (curr == tail) {
tail = prev;
}
size--;
}
}If we have a doubly linked list we can actually remove an element with a complexity of \(O(1)\). This is because we already have a reference to the previous element and don’t have to iterate our way through the list to find it.
public void remove(Node node) {
if (node == null) {
return;
}
if (node == head) {
head = head.next;
} else {
node.prev.next = node.next;
}
if (node == tail) {
tail = node.prev;
}
size--;
}Getting & Searching
To get an element at a specific index we have to iterate our way through the list to the index and then return the element. This has a complexity of \(O(n)\). In an array this operation is \(O(1)\) as you can just access the element at the index.
public E get(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException();
}
Node curr = head;
// iterate to the index
for (int i = 0; i < index; i++) {
curr = curr.next;
}
return curr.value;
}When searching for an element we have to iterate our way through the list to the element and then return it. This has a complexity of \(O(n)\). In an array this operation is \(O(n)\) or \(O(\log n)\) depending on whether the element stored has a canonic order and the array is sorted.
public Node search(E e) {
Node curr = head;
// iterate to the element
while (curr != null && !curr.value.equals(e)) {
curr = curr.next;
}
return curr;
}