Levenshtein Edit Distance

The Levenshtein edit distance problem is very similar to the longest common subsequence problem. However, they are not the same, the difference is that instead of finding the longest common subsequence we are looking for the minimum number of operations to transform one string into another. The operations we can perform are:

• Insert a character
• Remove a character
• Replace a character

So for example if we have the strings “TIGER” and “ZIEGE” the Levenshtein edit distance would be 3 as we can transform “TIGER” into “ZIEGE” by doing the following operations:

• Replace ‘T’ with ‘Z’ making the strings “ZIGER” and “ZIEGE”
• Inserting ‘E’ before ‘G’ to make “ZIEGER” and “ZIEGE”
• Removing ‘R’ to make “ZIEGE” and “ZIEGE”

There are many different operation combinations that would lead to the same result but the minimum number of operations is 3 and is what the Levenshtein edit distance is.

The ideas for the dynamic programming solution is very similar to the longest common subsequence problem. We create a 2D DP table where \(dp[i][j]\) will store the minimum number of operations to transform the substring of \(A\) ending at \(i\) into the substring of \(B\) ending at \(j\). But how do we know that a change we do when looking at \(A[i]\) and \(B[j]\) doesn’t effect the result or become redundant later on? For this let’s look at what happens to a character \(A[i]\) in the final result:

• If \(A[i]\) is removed in the final result then we can also do this as soon as we see \(A[i]\). So \(dp[i][j]=dp[i-1][j]+1\).
• If \(A[i]\) becomes a letter in \(B[1..j-1]\) then \(B[j]\) will at some point be inserted so we can do this as soon as we see \(B[j]\). So \(dp[i][j]=dp[i][j-1]+1\).
• If \(A[i]\) becomes \(B[j]\) then if this is already the case we don’t have to do anything but if it isn’t we can replace \(A[i]\) with \(B[j]\). So \(dp[i][j]=dp[i-1][j-1]+1\).

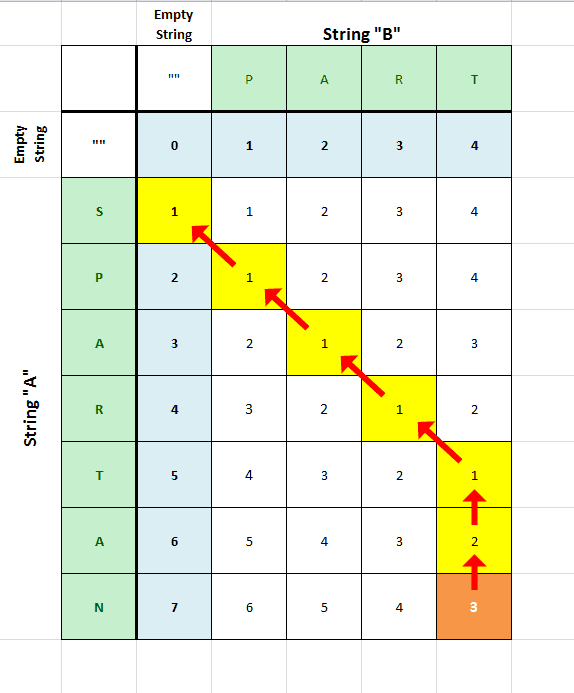
This leads to the 4 possible cases for each cell in the table and that the final answer will be stored in \(dp[m][n]\) where \(m\) and \(n\) are the lengths of \(A\) and \(B\) respectively.

public int minDistance(char[] A, char[] B) {
    int m = A.length;
    int n = B.length;
    int[][] dp = new int[m+1][n+1];
    // initialize the first row and column
    for (int i = 1; i <= m; i++) {
        dp[i][0] = i;
    }
    for (int j = 1; j <= n; j++) {
        dp[0][j] = j;
    }
 
    // fill the rest of the table
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (A[i-1] == B[j-1]) {
                dp[i][j] = dp[i-1][j-1];
            } else {
                dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1])) + 1;
            }
        }
    }
    return dp[m][n];
}

Again the time complexity of this solution is \(O(mn)\) where \(m\) and \(n\) are the lengths of the input strings \(A\) and \(B\) respectively. The space complexity is also \(O(mn)\) as we are storing the entire DP table. However, this isn’t necessary as we only need the previous row to calculate the current row so we can reduce the space complexity to \(O(\min(m,n))\) by only storing the previous row and the current row just like in the longest common subsequence problem.