Gaussian Elimination
The gaussian elimination algorithm, sometimes called the row reduction algorithm, is an algorithm that only uses certain elementary operations to solve a system of linear equations. The elementary operations are:
- Swapping two equations
- Multiplying an equation by a nonzero number, this also means we can divide an equation by a nonzero number as division is the same as multiplication by the reciprocal.
- Adding a row to another row. This can also be combined with the above operation of multiplying a row to be able to add a multiple of a row to another. The multiple can also be negative resulting in subtracting a multiple of one row from another row.
These operations are enough. When you are actually solving a system of linear equations by hand such as using the substitution method or the addition/subtraction method, you are actually performing exactly these operations.
Let’s look at an example to show why these operations are allowed and that they are the same as the conventional methods of solving systems of linear equations. We are given the following system of linear equations:
\[\begin{vmatrix} 2x - 2y + 4z = 6 \\ -5x + 6y -7z = -7 \\ 3x + 2y + z = 9 \end{vmatrix} \]You would probably solve it by trying to eliminate one variable at a time. For example let’s solve the first equation for \(x\):
\[\begin{align*} 2x = 2y - 4z + 6 \\ \rightarrow x = y - 2z + 3 \end{align*} \]Now we can substitute this into the second equation:
\[\begin{align*} -5x + 6y -7z &= -7 \\ -5(y - 2z + 3) + 6y - 7z &= -7 \\ -5y + 10z - 15 + 6y - 7z &= -7 \\ y + 3z &= 8 \end{align*} \]and the third equation:
\[\begin{align*} 3x + 2y + z &= 9 \\ 3(y - 2z + 3) + 2y + z &= 9 \\ 3y - 6z + 9 + 2y + z &= 9 \\ 5y - 5z &= 0 \end{align*} \]The above step could also have been achieved by addiding/subtracting the correct multiple of the first equation to the second and third equation, which is what the gaussian elimination algorithm does. To remove the \(x\) variable from the second equation we could subtract the first equation multiplied by \(-\frac{5}{2}\) from the second equation:
First we multiply the first equation by \(-\frac{5}{2}\):
\[\begin{align*} 2x - 2y + 4z &= 6 \\ -\frac{5}{2}(2x - 2y + 4z) &= -\frac{5}{2} \cdot 6 \\ -5x + 5y - 10z &= -15 \end{align*} \]Now we subtract this from the second equation:
\[\begin{align*} -5x + 6y -7z &= -7 \\ -5x + 6y -7z - (-5x + 5y - 10z) &= -7 - (-15) \\ y + 3z &= 8 \end{align*} \]And we have the same result as before. This process can be repeated for the third equation to get the same result as before. We can then also repeat the process to eliminate the \(y\) variable from the third equation by adding/subtracting the correct multiple of the second equation to the third equation.
Then to finally solve for the variables we can take the found value for \(z\) and substitute it into the second equation to solve for \(y\) and then substitute the found value for \(y\) and \(z\) into the first equation to solve for \(x\).
The Algorithm
We have seen that the operations are enough to solve a system of linear equations but how do we know that we aren’t effecting the solution by performing these operations?
The gaussian elimination algorithm works because the allowed operations do not change the solution set of the system of linear equations. Simply changing the order of the equations in the system is obvious why it doesn’t change the solution set. Adding an equation to another equation is allowed because imagine you have the following system of linear equations:
\[\begin{vmatrix} 5x + 3y = 200 \\ 2x + y = 100 \end{vmatrix} \]You can’t simple add 100 becuase you have to add the same amount to both sides of the equation and then the equation would no longer be in its standard form and by transforming it into its standard form you would have to subtract 100 from both sides of the equation which would result in a hole lot of nothing.
\[\begin{vmatrix} 5x + 3y + 100 = 300 \\ 2x + y = 100 \end{vmatrix} \]However, what you can do is add on the right side 100 to the first equation \(2x + y\) to left side because it is equal to 100. You can think of it as adding 100 to both sides but whilst keeping the equation in its standard form.
\[\begin{vmatrix} 5x + 3y + 2x + y = 200 + 100 \\ 2x + y = 100 \end{vmatrix} \rightarrow \begin{vmatrix} 7x + 4y = 300 \\ 2x + y = 100 \end{vmatrix} \]Multiplying an equation by a nonzero number is allowed because it is the same as multiplying both sides of the equation by the same number, it doesn’t change the linear equation at all.
Combining these two operations, we can see that we can add a multiple of one equation to another equation and it will not change the solution set!
So now that we are convinced that the operations are allowed and the algorithm should work, let’s see what we have to do to use the algorithm and solve a system of linear equations. For now we will only look at systems of linear equations that have the same number of equations as variables. So they are not over or underdetermined.
Before the algorithm can be used to solve a system of linear equations, the system is transformed into a matrix, to be more specific, an augmented matrix. If we have a system of linear equations with \(n\) variables and \(n\) equations, we create a matrix with \(n\) rows and \(n+1\) columns. The first \(n\) columns contain the coefficients of the variables in the equations. So the first row of the matrix matches the first equation in the system of linear equations. If in the first equation the first variable has a weight/coefficent of 2, then the first entry in the first row of the matrix is 2. This process is continued for all the variables in the equation. The last column of the matrix contains the constants on the right side of the equations in the general form. For visibility, a vertical line is drawn between the last column of the matrix and the rest of the columns. This vertical line is not part of the matrix, it is just there to show that the last column contains the constants.
The system of linear equations:
\[\begin{vmatrix} 2x + 3y = 6 \\ x - y = \frac{1}{2} \end{vmatrix} \]Has the coefficient matrix:
\[\begin{bmatrix} 2 & 3 \\ 1 & -1 \end{bmatrix} \]And the augmented matrix:
\[\left[\begin{array}{cc|c} 2 & 3 & 6 \\ 1 & -1 & \frac{1}{2} \end{array}\right] \]Once we have the augmented matrix, we can use the gaussian elimination algorithm to solve the system of linear equations.
Row Echelon Form
If you were given the following system of linear equations you would probably be able to solve the system very easily:
\[\begin{vmatrix} 2x + 3y + 4z = 19 \\ 5y + 6z = 17 \\ 7z = 14 \end{vmatrix} \]The reason for this is that the last equation can be solved without any real work for \(z = 2\). Then you can substitute this value into the second equation to solve for \(y = 1\) and then substitute the values for \(y\) and \(z\) into the first equation to solve for \(x = 4\).
If we look at the coefficent matrix of the system of linear equations we can see that the matrix is an upper triangular matrix.
\[\begin{bmatrix} 2 & 3 & 4 \\ 0 & 5 & 6 \\ 0 & 0 & 7 \end{bmatrix} \]This is not a coincidence and is the reason why the gaussian elimination algorithm tries to transform the augmented matrix into such a matrix. However, a triangular matrix is only defined for square matrices, so we have to look at a more general form of the matrix, the row echelon form.
For a matrix to be in row echelon form it needs to satisfy the following conditions:
- The first nonzero element in each row, called the leading entry or pivot, is to the right of all the pivots of the rows above it.
- All rows that only contain zeros are at the bottom of the matrix.
In row echelon form:
\[\begin{bmatrix} 1 & 2 & 3 & 4 \\ 0 & 2 & 2 & 3 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix} \]Notice that in the third row, the pivot is not directly to the right of the pivot in the second row, but it is to the right it doesn’t matter if there are zeros in between.
Not in row echelon form:
\[\begin{bmatrix} 1 & 2 & 3 & 4 \\ 0 & 2 & 2 & 3 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix} \]Because in the third row, the pivot is not to the right of the pivot in the second row.
Elimination
The goal of the gaussian elimination algorithm is to transform the augmented matrix into row echelon form. We do this using the allowed operations we have already seen above for normal systems of linear equations, now they are just matrix operations, these can however be thought of as applying the operations to the system of linear equations under the hood. The matrix operations are as follows:
- Swap two rows
- Multiply a row by a nonzero number, this also means we can divide a row by a nonzero number
- Add a multiple of one row to another row, this can also be combined with the above operation of multiplying a row to be able to add a multiple of a row to another row or subtract a multiple of one row from another row.
The process of transforming the augmented matrix into row echelon form is called elimination. The elimination process is as follows:
- We start at the first column and find the first nonzero element. This will be our pivot element. If the first row doesn’t have a pivot element, we swap the first row with a row that has a pivot element in the first column.
- Now we want to eliminate all the elements below the pivot element. We do this by subtracting or adding a multiple of the row with the pivot element from the rows below it.
- Once we have eliminated all the elements below the pivot element, we move to the next column. However, here we only look at the rows below the pivot element of the previous column. So the second row. We repeat the process of finding the pivot element and eliminating the elements below it until we have reached the second to last column.
We might have a case where have to swap rows to get the pivot element in the correct position:
Solving a System of Linear Equations
Now that we have our augmented matrix in row echelon form, we can solve the system of linear equations by reading the solution directly for the last variable and then substituting the found value into the previous row to solve for the next variable. This process is called back substitution as we are substituting the found values back into the previous rows.
However, the gaussian elimination algorithm doesn’t always work. There are cases where the algorithm fails. For example if the matrix can not be transformed into row echelon form. This can also happen if we have rows with only zeros in the coefficient matrix but the constant is not zero. This would be an unsolvable equation as we can not make the left side of the equation equal to the right side of the equation.
Compacted Form
When working with large matrices, having to write out all the rows and columns for each operation can be cumbersome. To make it easier to work with large matrices, it can be useful to compact the matrix by only looking at the columns that still need to be processed.
LU Decomposition
Each row operation that is performed in the gaussian elimination algorithm can be represented as a matrix multiplication. We know that if we multiply a matrix by an identity matrix we get the same matrix. We also seen permutation matrices that can be used to swap rows which is one of the operations that can be performed in the gaussian elimination algorithm. The other operations can be summarized to adding a multiple of one row to another row. This operation can also be represented as a matrix multiplication. For a matrix \(\boldsymbol{A}\in \mathbb{R}^{3 \times 3}\) we can add a \(c_1\) times the first row to the second row by multiplying the matrix with the following matrix:
\[\begin{bmatrix} 1 & 0 & 0 \\ c_{21} & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \]To then subtract \(c_2\) times the first row from the third row we multiply the matrix with the following matrix:
\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -c_{31} & 0 & 1 \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \]This is the same as adding a negative multiple of the first row to the third row. We can apply these operations one after another to in the end get the upper triangular matrix that we get from the gaussian elimination algorithm. If we denote these elimination matrices that we multiply with as \(\boldsymbol{E}_1, \boldsymbol{E}_2, \ldots, \boldsymbol{E}_n\) and the resulting matrix as \(\boldsymbol{U}\) we can write the following:
\[E_n \ldots E_2 E_1 \boldsymbol{A} = \boldsymbol{U} \]So if we always had to subtract some value from the rows we would get something like this:
\[\begin{align*} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -c_{32} & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -c_{31} & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ -c_{21} & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \boldsymbol{A} &= \boldsymbol{U} \begin{bmatrix} 1 & 0 & 0 \\ -c_{21} & 1 & 0 \\ c_{32}c_{21}-c_{31} & -c_{32} & 1 \end{bmatrix} \boldsymbol{A} = \boldsymbol{U} \end{align*} \]This isn’t a very nice matrix. However, the inverse of the elimination matrix is nice. By left multiplying the inverse of the elimination matrix we come to the following:
\[\begin{align*} \boldsymbol{A} = \begin{bmatrix} 1 & 0 & 0 \\ c_{21} & 1 & 0 \\ c_{31} & c_{32} & 1 \end{bmatrix} \boldsymbol{U} \end{align*} \]Where \(c_{21}\) etc. are the multipliers that we use to subtract the multiple of the first row from the other rows (if we have to add a multiple of the first row we would have a negative multiplier). Notice that the matrix that we multiply with is a lower triangular matrix. This is the idea of the LU decomposition where the matrix \(\boldsymbol{A}\) is factorized into a product of a lower triangular matrix \(\boldsymbol{L}\) and an upper triangular matrix \(\boldsymbol{U}\):
\[\boldsymbol{A} = \boldsymbol{LU} \]But what is the advantage of this factorization? The advantage is that we can solve the system of linear equations \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}\) very efficiently for any \(\boldsymbol{b}\). First we calculate the two matrices using the gaussian elimination algorithm. For this we just focus on the coefficent matrix and not the augmented matrix. The operations that we perform we store/memorize by storing the multipliers in the lower triangular matrix.
We first solve \(\boldsymbol{L}\boldsymbol{y} = \boldsymbol{b}\) for \(\boldsymbol{y}\) with forward substitution because \(\boldsymbol{L}\) is a lower triangular matrix. Then we solve \(\boldsymbol{U}\boldsymbol{x} = \boldsymbol{y}\) for \(\boldsymbol{x}\) with back substitution because \(\boldsymbol{U}\) is an upper triangular matrix.
Partial Pivoting
The matrix A can be permuted with a permutation matrix P to swap rows.
\[PA = LU \]Where P is a permutation matrix, A is the matrix we want to factorize, L is the lower triangular matrix and U is the upper triangular matrix.
This is called partial pivoting because we only swap rows.
What is the optimal strategy for choosing the pivot element? Maybe this should actually be written in the gaussian elimination method.
Full Pivoting
The matrix A can be permuted with permutation matrices P and Q to swap rows and columns.
\[PAQ = LU \]Where P and Q are permutation matrices, A is the matrix we want to factorize, L is the lower triangular matrix and U is the upper triangular matrix.
This is called full pivoting because we swap rows and columns.
LDU Decomposition
The LU decomposition can be extended to the LDU decomposition where D is a diagonal matrix.
\[A = LDU \]Where A is the matrix we want to factorize, L is the lower triangular matrix, D is the diagonal matrix and U is the upper triangular matrix.
What are the advantages?
Gauss-Jordan Elimination
The Gaussian Elimination Algorithm above was only defined for linear systems of equations with the same number of equations as variables. The Gauss-Jordan Elimination Algorithm is an extension of the Gaussian Elimination Algorithm that can be used to solve linear systems of equations with \(m\) equations and \(n\) variables. The Gauss-Jordan Elimination Algorithm is used to find the reduced row echelon form of a matrix. The idea is very much the same as the gaussian elimination however we do a bit more work to learn more about the matrix.
Reduced Row Echelon Form
Reduced row echelon form is a stricter form of row echelon form. A matrix is in reduced row echelon form if it satisfies the following conditions:
- It is in row echelon form.
- The pivot element in each row is equal to 1, called a leading 1.
- Each column containing a leading 1 has zeros in all other positions, so the column is a standard unit vector.
The previous matrix that was in row echelon form is not in reduced row echelon form. To get it into reduced row echelon form we have to divide the rows by the pivot element so we get leading 1’s and then subtract the rows from each other to get zeros in the positions above and below the leading 1’s and lastly remove the rows that only contain zeros.
\[\begin{bmatrix} 1 & 2 & 3 & 4 \\ 0 & 2 & 2 & 3 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix} \]This matrix is in reduced row echelon form.
\[\begin{bmatrix} 1 & 0 & 3 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \]The Algorithm
Solving a System of Linear Equations
Free Variables
the columns that do not contain a pivot are called free variables. The number of free variables is equal to the number of columns minus the number of pivots.
Number of Solutions
using the rank of the matrix we can determine the number of solutions to a system of linear equations.
Meaning of regular and singular matrices???
Also something about homogenous systems and non-homogenous systems. Trivial solutions and non-trivial solutions.
Consistency conditions
Calculating the Inverse via Gaussian Elimination
The gaussian elimination method can be extended to calculate the inverse of a matrix. Because the inverse of a matrix is only defined for square matrices, this algorithm only works for square matrices such as \(2 \times 2\) matrices, \(3 \times 3\) matrices, \(\boldsymbol{A} \in \mathbb{R}^{n \times n}\).
Just like when solving a system of linear equations, we first transform the matrix into an augmented matrix. However, instead of having the constants on the right side of the vertical line we add the identity matrix \(\boldsymbol{I}\) of the same size as the matrix on the right side of the vertical line.
Given the matrix:
\[\boldsymbol{A} = \begin{bmatrix} 2 & 4 & -2 \\ 4 & 9 & -3 \\ -2 & -3 & 7 \end{bmatrix} \]We can calculate the inverse of \(\boldsymbol{A}\) by transforming it into the following augmented matrix:
\[[\boldsymbol{A}|\boldsymbol{I}] =\left[\begin{array}{ccc|ccc} 2 & 4 & -2 & 1 & 0 & 0 \\ 4 & 9 & -3 & 0 & 1 & 0 \\ -2 & -3 & 7 & 0 & 0 & 1 \end{array}\right] \]The goal of the algorithm is now to transform the left side of the augmented matrix into the identity matrix \(\boldsymbol{I}\). We are still only allowed to perform the same operations as before:
- Swapping two rows
- Multiplying a row by a nonzero number
- Adding a multiple of one row to another row, the multiple can also be negative resulting in subtracting a multiple of one row from another row.
Important it is important that when we perform an operation on the left side of the augmented matrix, we also perform the same operation on the right side!
By then transforming the left hand side firts into row echelon form and then into reduced row echelon form and then lastly performing back substitution we should get on the left hand side the identity matrix \(\boldsymbol{I}\) and on the right hand side the inverse of the matrix \(\boldsymbol{A}\) so that we have:
\[[\boldsymbol{I}|\boldsymbol{A}^{-1}] \]Which fullfills the definition of the inverse of a matrix:
\[\boldsymbol{A} \boldsymbol{A}^{-1} = \boldsymbol{I} \]This gives us the inverse of the matrix \(\boldsymbol{A}\):
\[\boldsymbol{A}^{-1} = \begin{bmatrix} \frac{27}{4} & -\frac{11}{4} & \frac{3}{4} \\ -\frac{11}{4} & \frac{5}{4} & -\frac{1}{4} \\ \frac{3}{4} & -\frac{1}{4} & \frac{1}{4} \end{bmatrix} = \frac{1}{4} \begin{bmatrix} 27 & -11 & 3 \\ -11 & 5 & -1 \\ 3 & -1 & 1 \end{bmatrix} = \begin{bmatrix} 6.75 & -2.75 & 0.75 \\ -2.75 & 1.25 & -0.25 \\ 0.75 & -0.25 & 0.25 \end{bmatrix} \]CR-Decomposition
Just like any natural number can be factored or decomposed into its prime factors, any matrix can also be decomposed into other matrices. For example the number 1001 can be decomposed into its prime factors:
\[1001 = 7 \cdot 11 \cdot 13 \]For natural numbers the prime factorization can reveal a lot about the number, for example, if the number is a prime number or not or if given two numbers the greatest common divisor can be found. For example for the numbers 1001 and 2002:
\[\begin{align*} 1001 &= 7 \cdot 11 \cdot 13 \\ 2002 &= 2 \cdot 7 \cdot 11 \cdot 13 gcd(1001, 2002) = 7 \cdot 11 \cdot 13 = 1001 \end{align*} \]The idea of decomposing a matrix into other matrices is similar, it can reveal a lot about the matrix. Our first decomposition is the CR-decomposition, where the idea is as follows. Given a matrix \(\boldsymbol{A} \in \mathbb{R}^{m \times n}\) of rank \(r\), we can decompose it into two matrices \(\boldsymbol{C} \in \mathbb{R}^{m \times r}\) and \(\boldsymbol{R} \in \mathbb{R}^{r \times n}\) such that:
\[\boldsymbol{A} = \boldsymbol{C} \boldsymbol{R} \]If we look at an example we might get an idea of how we find the matrices \(\boldsymbol{C}\) and \(\boldsymbol{R}\). Let’s say we have the following matrix:
\[\boldsymbol{A} = \begin{bmatrix} 1 & 2 & 0 & 3 \\ 2 & 4 & 1 & 4 \\ 3 & 6 & 2 & 5 \end{bmatrix} \]We can see that the matrix has rank 3, as the second column is just double the first column and the fourth column is a linear combination of the first and third column. So we know we can create all the columns from the first and the third column, the independent columns. So let’s add them all to make a matrix.
\[\boldsymbol{C} = \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ 3 & 2 \end{bmatrix} \]Now the question is with what can be multiply the matrix \(\boldsymbol{C}\) to get the matrix \(\boldsymbol{A}\). We know that the matrix vector product is a linear combination of the columns of the matrix. So the \(i\)-th entry of the vector is the weight of the \(i\)-th column of the matrix. We also know that the matrix multiplication is like creating multiple linear combinations of the columns of the matrix. So we can see that the matrix \(\boldsymbol{R}\) is the matrix that contains the weights of the independent columns to create all the columns of the matrix \(\boldsymbol{A}\). For the example above this looks like this:
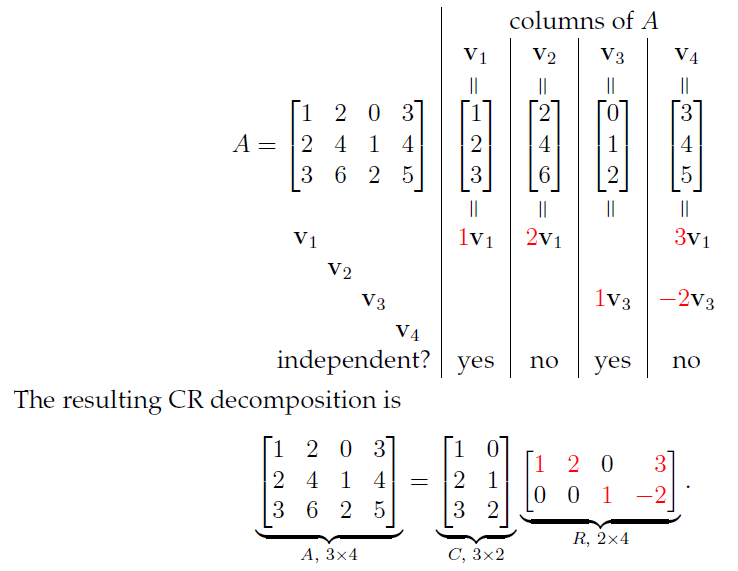
You might notice something about the matrix \(\boldsymbol{R}\), it is the exact matrix that we get when we perform the gauss-jordan algorithm after removing the zero rows at the bottom so the reduced row echelon form of the matrix. Why is this?
Precise explanation as to why this is the case, has to do with the fact of the row operations
So after performing the gauss-jordan algorithm on the matrix \(\boldsymbol{A}\) we can easily find the matrices \(\boldsymbol{C}\) and \(\boldsymbol{R}\). The matrix \(\boldsymbol{C}\) is the matrix that contains the independent columns which are the columns that have a pivot element. The matrix \(\boldsymbol{R}\) is the matrix that contains the weights of the independent columns to create all the columns of the matrix \(\boldsymbol{A}\) which corresponds to the reduced row echelon form of the matrix that we get after performing the gauss-jordan algorithm.