Discrete Random Variables

Zufallsvariablen

Eine Zufallsvariable $X$ ist eine Funktion welche jedem Elementarereignis $\omega \in \Omega$ genau eine reele Zahl zuordnet. Wir unterscheiden noch dabei, ob eine Zufallsvariable diskret oder stetig ist. Hier werden wir diskrete Zufallsvariablen anschauen später werden wir noch stetige dazu nehmen.

Diskrete Zufallsvariablen

Eine diskrete Zufallsvariable kann endlich viele oder abzählbar unendliche viele Werte annehmen. Gute Beispiel dafür sind Ergebnisse beim Würfeln, Anzahl Münzwurfe bis zum ersten Mal Kopf etc.

Eine gute Videoerklärung dazu gibt es auch hier (opens in a new tab).

Dichte/Wahrscheinlichkeits-Funktion

Bei einer diskreten Zufallsvariable gehört zu jedem Wert $x_i$ eine bestimmte Wahrscheinlichkeit $P(X=x_i)$. Diese Beziehung lässt sich gut mit einer sogenannten Verteilungstabelle oder einem Stabsdiagramm (Wahrscheinlichkeitsdiagramm) visualisieren, dabei gilt

Eine Dichtefunktion ist auch normiert, das heist, dass alle Wahrscheinlichkeiten der verschiedenen Werte $x_i$ der Zufallsvariable $X$ zusammen 1 ergeben.

Verteilungstabelle:

Stabsdiagramm:

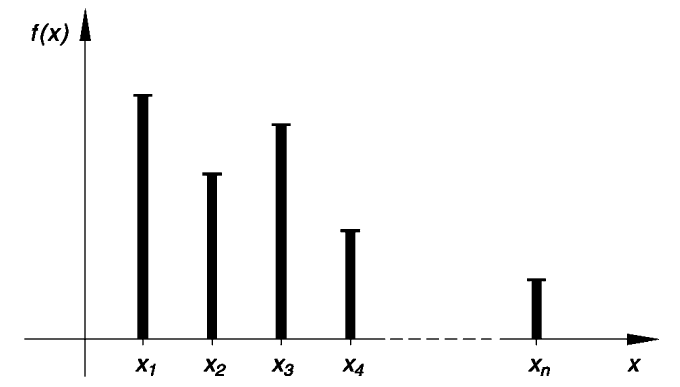
mehr dazu findest du hier (opens in a new tab).

Verteilungsfunktion

Die Verteilungsfunktion $F(x)$ einer Zufallsvariable $X$ ist die Wahrscheinlichkeit dafür, dass die Zufallsvariable $X$ einen Wert, der kleiner oder gleich $x$ annimmt.

Die Wahrscheinlichkeit bei einer diskreten Zufallsvariable $P(a < X \leq b)$ ist gegeben durch $F(b)-F(a)$

mehr dazu findest du hier (opens in a new tab).

Erwartungswert

Der Erwartungswert ist der Wert, den wir im Durchschnitt erwarten können und ist definiert als

Erwartungswerte addieren

Erwartungswert, Skalar multiplizieren

Erwartungswert, Skalar addieren

Erwartungswert, Funktion anwenden

Für all Funktionen $g: \mathbb{R} \mapsto \mathbb{R}$

Varianz

Wenn wir den Erwartungswert von $X$ als $\mu$ beschreiben, dann ist die Varianz gegeben durch

oder auch in kurz

Varianz, Skalar addieren

Varianz, Skalar multiplizieren

Standardabweichung

Die Standardabweichung ist gegeben durch

Diskrete Verteilungen

Nun schauen wir uns ein paar Verteilungen, an die häufig vorkommen, wenn man mit diskreten Zufallsvariablen arbeitet.

Binomial-Verteilung

Die Binomialverteilung der Zufallsvariable $X$ ist die Anzahl Treffer bei der $n$-maligen unabhängigen Durchführung eines Experiments mit 2 Elementarereignisse, Treffer und kein Treffer wobei $p$ die Wahrscheinlichkeit für einen Treffer ist.

• Wir schreiben dann $X \sim Bin(n,p)$
• Die Dichtefunktion von $X$ ist $f(k)=\binom{n}{k}p^k(1-p)^{n-k}$ wobei $k$ die Anzahl benötigter treffer ist.
• $E(X) = n \cdot p$
• $V(X) = n \cdot p \cdot (1-p)$

In Matlab haben wir die Funktionen:

• Dichtefunktion $binopdf(k,n,p)$ wobei $pdf$ English ist und für "probability density function" steht
• Verteilungsfunktion $binocdf(k,n,p)$ wobei $cdf$ English ist und für "cumulative distribution function" steht

mehr dazu findest du hier (opens in a new tab).

Bernoulli-Verteilung

Die Bernoulli-Verteilung ist eine spezielle Form der Binomialverteilung wobei $n=1$. Wir können dann alles ein wenig vereinfachen.

• Wir schreiben dann $X \sim B(p)$
• Die Dichtefunktion von $X$ ist $f(0)= 1-p, f(1)=p$
• $E(X) = p$
• $V(X) = p \cdot (1-p)$

mehr dazu findest du hier (opens in a new tab).

Geometrische-Verteilung

Die Geometrische Verteilung der Zufallsvariable $X$ ist die Anzahl der Versuche bis zum ersten Treffer bei der wiederholten unabhängigen Durchführung eines Experiments mit 2 Elementarereignisse, Treffer und kein Treffer wobei $p$ die Wahrscheinlichkeit für einen Treffer ist.

• Wir schreiben dann $X \sim Geo(p)$
• Die Dichtefunktion von $X$ ist $f(k)=\binom{n}{k}p\cdot (1-p)^{k-1}$ wobei $k$ bedeutet, dass die ersten $k-1$ Versuche kein Treffer waren aber der $k$-te Versuch ein Treffer ist.
• $E(X) = \frac{1}{p}$
• $V(X) = \frac{1-p}{p^2}$

In Matlab haben wir die Funktionen:

• Dichtefunktion: $geopdf(k-1,p)$
• Verteilungsfunktion $geoocdf(k-1,p)$

mehr dazu findest du hier (opens in a new tab).

Hypergeometrische-Verteilung

Die Hypergeometrische Verteilung der Zufallsvariable $X$ ist die Verteilung, die beim $n$-maligen Ziehen ohne Zurücklegen und ohne Reihenfolge aus einer Urne mit $N$ Kugeln, von denen $M$ eine spezielle Eigenschaft haben und wo die Anzahl der gezogenen Kugeln mit dieser speziellen Eigenschaft gezählt werden.

• Wir schreiben dann $X \sim Hyp(N,M,n)$
• Die Dichtefunktion von $X$ ist $f(k)=\binom{M}{k} \cdot \frac{\binom{N-M}{n-k}}{ \binom{N}{n}}$ wobei $N$ die Gesamtanzahl der Kugeln ist, $M$ die Anzahl mit der speziellen Eigenschaft. $n$ ist dann der Umfang der Stichprobe also die Anzahl der entnommenen Kugeln und $k$ die Anzahl angestrebte Kugeln mit der speziellen Eigenschaft.
• $E(X) = n \cdot \frac{M}{N}$
• $V(X) = n \cdot \frac{M}{N} \cdot (1 - \frac{M}{N}) \cdot \frac{N-n}{N-1}$

In Matlab haben wir die Funktionen:

• Dichtefunktion: $hygepdf(k,N,M,n)$
• Verteilungsfunktion $hygecdf(k,N,M,n)$

mehr dazu findest du hier (opens in a new tab).

Poisson-Verteilung

Die Poisson-Verteilung kommt bei Zufallsvariablen zum Einsatz, welche die Anzahl der Ereignisse einer bestimmten Art in einem Zeit- und/oder Ortsintervall beschreiben die Anzahl dieses Ereignisses entspricht $\lambda$. Diese Ereignisse sind oftmals "seltene" Ereignisse z.B.

• $X$ Anzahl Druckfehler auf einer Seite eines Buchs
• $X$ Anzahl Unfälle an einem Wochenende in einem Skigebiet
• $X$ Anzahl falsch gewählter Telefon-Nummern an einem Tag
• $X$ Anzahl Erdbeben in einem Jahr in einer bestimmten Region.

Dies sind nur ein paar Beispiele der Poisson-Verteilung, sie ist einer der wichtigsten Verteilungen die wir kennen.

• Wir schreiben dann $X \sim Poi(\lambda)$
• Die Dichtefunktion von $X$ ist$f(k)=\frac{\lambda^k}{k!} \cdot e^{-\lambda}$
• $E(X) = \lambda$
• $V(X) =\lambda$

In Matlab haben wir die Funktionen:

• Dichtefunktion: poisspdf(k,$\lambda$)
• Verteilungsfunktion poisscdf(k,$\lambda$)

mehr dazu findest du hier (opens in a new tab)