Binary Search Trees

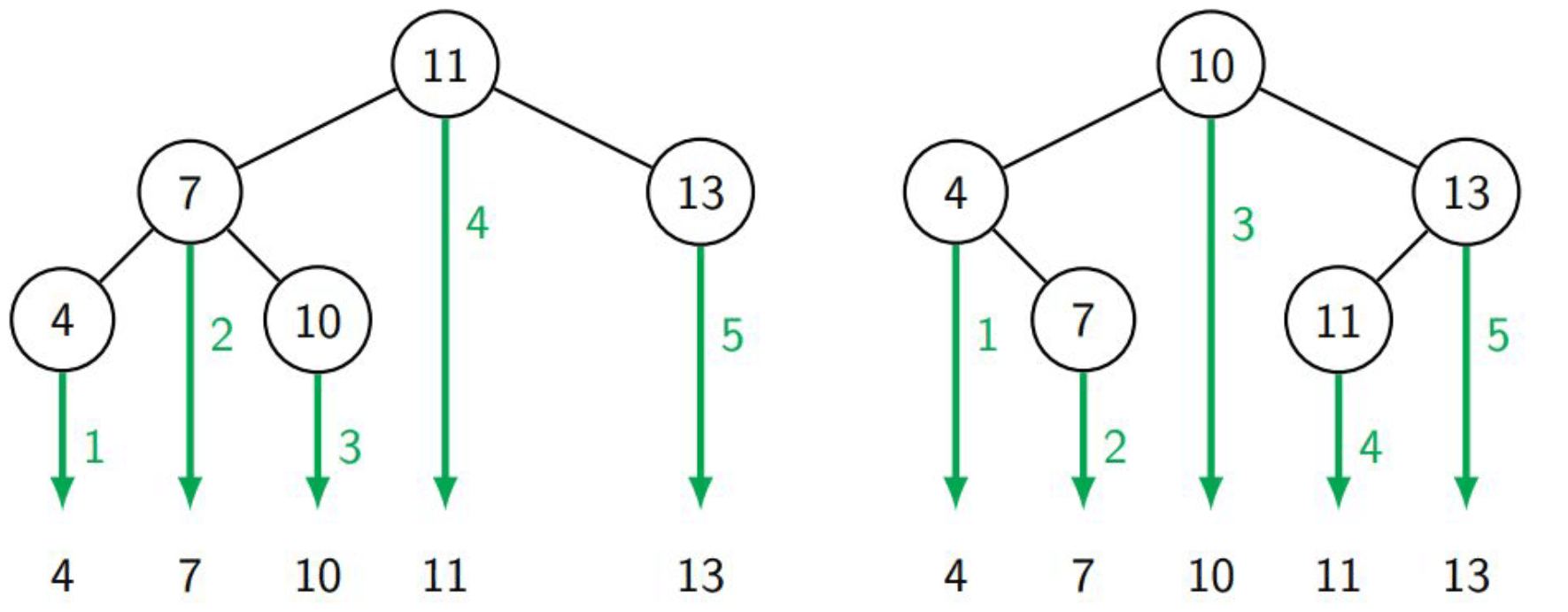
A binary search tree is a binary tree where each node has a key. key(v)=Key of the node v. The important thing here is that in the left subtree of a node there are only nodes with keys that are smaller than the key of the node. In the right subtree accordingly only nodes with a key that are the same or larger.

Interestingly when traversing the tree in-order we can see that the keys ascend.

Operations

Insert

When inserting a node you need to find the ideal place for insertion. This is started by comparing it with the root and seeing whether it belongs in the left or right half. This is then repeated recursively repeated until the insertion point is found.

Search

When searching for a specific key we follow a similar process as with when inserting. By comparing the key with the roots key and then carrying on down the tree. If we don't just want the first node but all nodes with this key, once the first node is found we carry on down the right subtree until it is empty.

Remove

When removing a node we distinguish between 3 different cases.

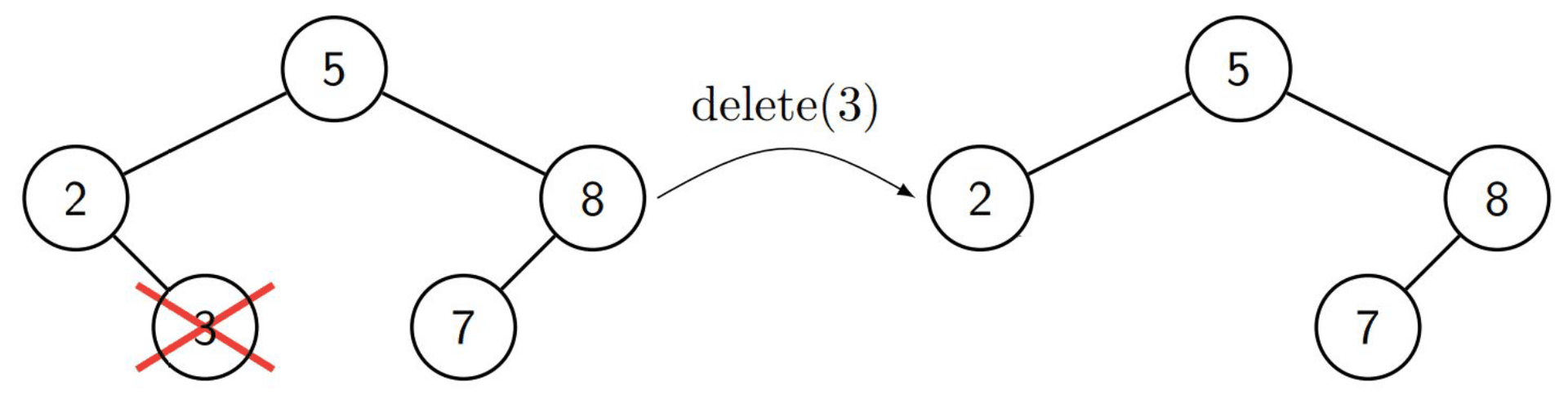
Leaf

We search for the node and then simply remove it, nothing complicated.

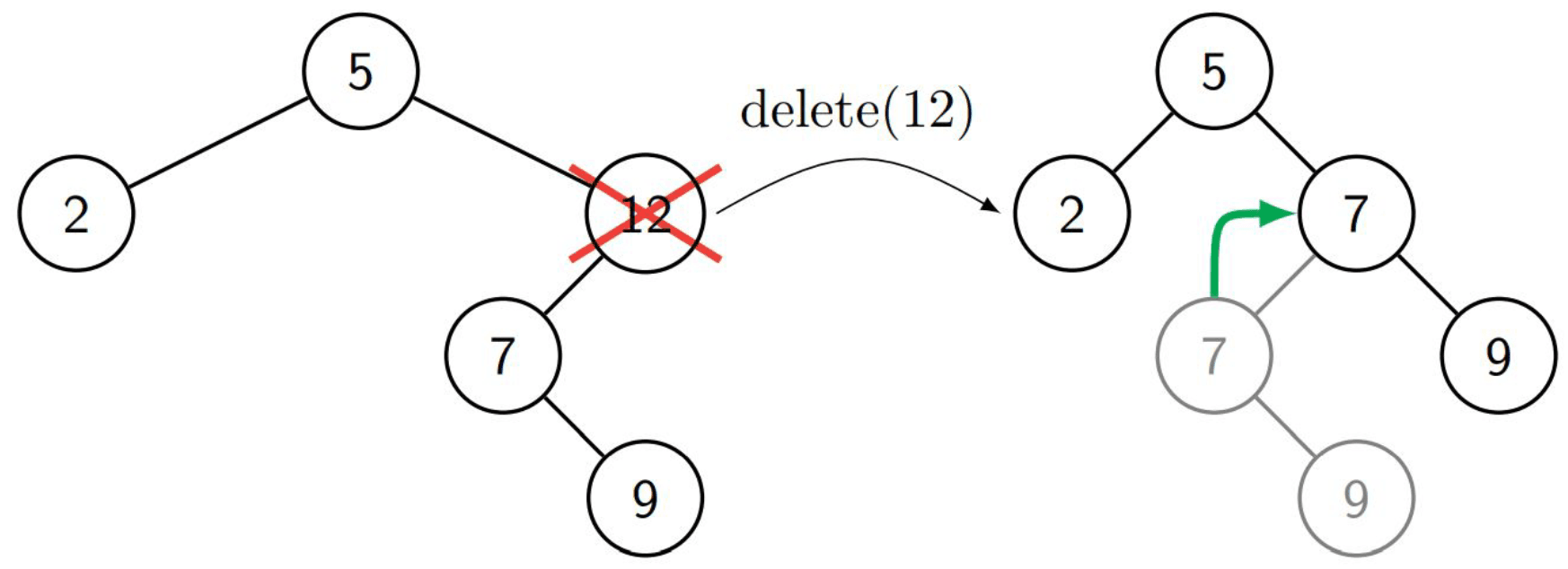
Node with 1 child

We search for the node to be removed and remove it. The child of the removed node then takes its place. Also nothing complicated.

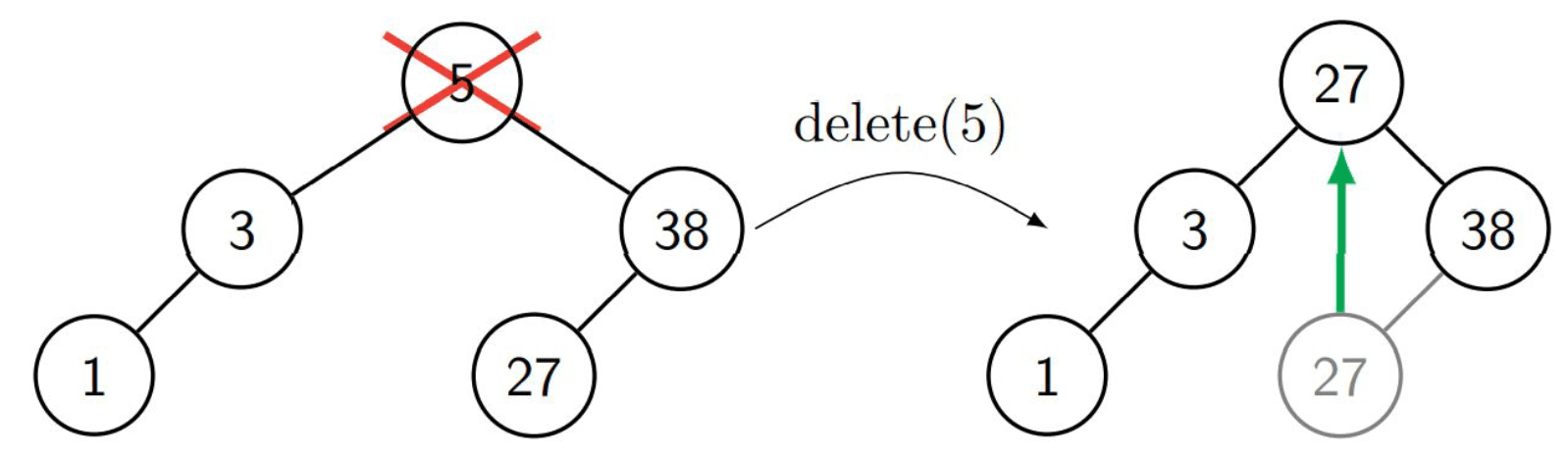
Node with 2 children

We search for the node to be removed. We then look for the symmetrical (inorder) successor, which is the node in the right subtree that is the furthest left. We then replace the to be removed node with the symmetrical successor. Lastly we delete the symmetrical successor at its original position which is either case 1 or 2.

private Node<K, E> remove(Node<K,E> node, K key){
 if (node == null) {
  return null;
 }
 else {
  int c = key.compareTo(node.key);
  if (c < 0) {
   node.left = remove(node.left, key);
  }
  else if (c > 0) {
   node.right = remove(node.right, key);
  }
  else {
   if (node.left == null) {
    node = node.right;
    nodeCount--;
   }
   else if (node.right == null) {
    node = node.left;
    nodeCount--;
   }
   else {
    Node<K, E> succ = symSucc(node.right);
    succ.right = remove(node.right, succ.key);
    succ.left = node.left;
    node = succ;
   }
  }
  return node;
 }
}
 
private Node<K, E> symSucc(Node<K,E> node){
 Node<K, E> succ = node;
 while (succ.left != null) {
  succ = succ.left;
 }
 return succ;
}

Time complexities

The time complexities of the operations depend on the height of the tree. In the worst case all operations take O(n), when the tree has become like a list. In the best case all operations O(log n), this is when the tree is complete(excluding the last level). From this we can see it is important to keep the height as small as possible to have the best time complexities.