Heaps
Priority queue
In a lot of cases we want a queue that is however influenced by a priority. The priority is the key of an element and must be comparable. The elements in the queue are then sorted by this priority resulting in HIFO, highest priority in first out. There are then 3 operations that can be performed on this priority queue. Elements can be added, we can look at the element with the highest priority and remove it. Depending there are then 2 ways in which we can define the key with the highest priority, either it is the largest or smallest key, which then lead to the following definitions:
A Minimum Priority Queue where peek()=min() and remove()=removeMin() or a Maximum Priority Queue where peek()=max() annd remove()=removeMax().
Priorities
A priority can contain any element that has a comparable key.
Element can either have a natural or predefined key and order. For example if the element is a number then the number can be used as its key. However if the element is a clubmember then we might use the amount of years he has been a member as the key. It gets tricky with role hierarchies for example in the military. So we can define the Interface like the following
public interface MinPriorityQueue<K extends Comparable<? super K>> {
boolean add(K element);
K min();
K removeMin();
int size();
}importantly here is the extends Comparable
We might not have predefined priorities but priorities we assign when adding.
Min-Heap
A Min-Heap is a complete binary tree with the exception of the last level. On the last level it is filled from left to right. Importantly each nodes key is smaller or equal to that of its children.

Just with this definition we can already easily implement 2 of the methods in the interface we defined both with O(1). The min() method is just the root and the size() method is done just like in all other collections with a counter.
Add
We start by adding the new element to the furthest left free space on the lowest level or if it is already full left on a new level. To then correct the order the element slowly wanders up the tree by swapping with its parents until it is larger then its parent or is in the root. This process of wandering up the tree we call sift up. O(log n) = O(1)+O(log n)

RemoveMin
We already know that the min element is the root so we can remove it. We then replace it with the furthest right element on the last level and let it sink down the tree, meaning we swap it with its smaller child until it is smaller then both of its children or is a leaf. This process of sinking down the tree we call sift down. O(log n) = O(1)+O(log n)
Array Representation
We can also represent a Min-Heap as an array.
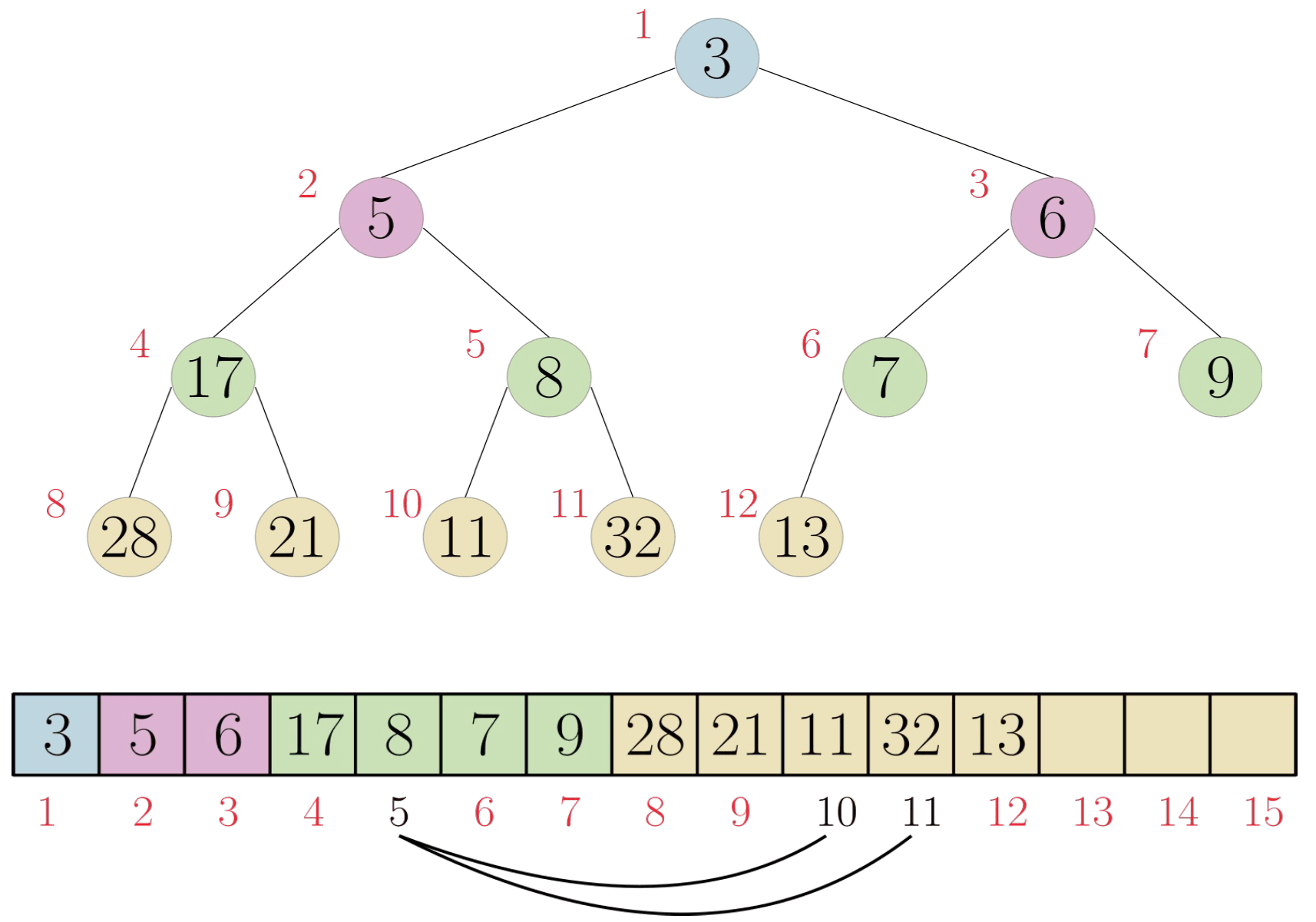
We can then see the following relationships for a node with the index . These are all int operations so we ignore decimal points when deviding.
| Root at index 1 | Root at index 0 | |
|---|---|---|
| Parent Node of i | i/2 | (i-1)/2 |
| Left child of i | 2i | 2i+1 |
| Right child of i | 2i + 1 | 2i+2 |
| Indexes of all leaves | size/2+1 till size | size/2till size -1 |
Building a heap from a filled array
The first idea is we want to add one element after another from front to back, so in the top down. We however notice that we save a bit of space but it takes O(n log n). So we need a second idea.
Floyd's heap construction
Here instead of a lot of elements having to be sifted up we let the elements sift down which then leads to an algorithm that is O(n).
Heap(HeapNode<K>[] elems) {
this.heap = elems;
this.size = elems.length;
for(int i=size/2; i>= 0; i--){
siftDown(i);
}
}Sorting using a heap (Heapsort)
This is the so called heapsort. We take an array and by using floyds heap construction, construct a heap. We can then just for the size of the array removeMin which leads to a time complexity of O(n log n) since the removeMin is O(log n). However we do need to have O(n) additional space. However this can be improved to O(1) if we construct the heap directly in the input array and add the removeMin and add it to the back of the input array so we at the end of the array we have sorted array.
