Broadcasting

Broadcasting is something special that computer scientists make use of when working with tensors such as scalars, vectors and matrices. It's very useful for computer scientists but it is not really mathematical. It allows libraries like numpy to perform arithmetic operations (element-wise addition or multiplication, also known as hadamard product) although the arrays have different shapes. If the arrays meet certain constraints then the smaller array is “broadcast” across the larger array so that they have compatible shapes to perform the operation. Let's look at some simple examples of how broadcasting in numpy (opens in a new tab) works. We might often want to perform the element-wise multiplication between two different arrays, in this case, vectors of the same shape this works fine.

import numpy as np
 
a = np.array([1.0, 2.0, 3.0])
b = np.array([2.0, 2.0, 2.0])
a * b

    array([2., 4., 6.])

But what about multiplying a vector with a scalar? This is defined mathematically but in numpy these two arrays do not have the same shape yet it still works.

b = 2
a * b

    array([2., 4., 6.])

The result is the same as where b was an array consisting of only the value 2. So in this case numpy transformed the integer 2 to np.array([2]) to perform the operation but it also performed broadcasting which we can think of as the array containing the single value 2 being stretched to the same shape as a. The new elements in b are just copies of the original scalar.

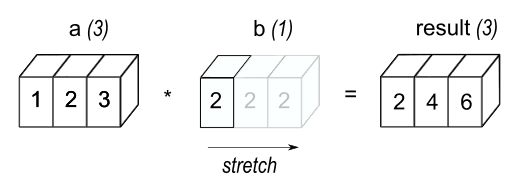
A visualization of the "stretching" when broadcasting an array.

Info

The stretching analogy is only conceptual. NumPy is smart enough to use the original scalar value without actually making copies so that broadcasting does not waste memory.

Conditions for Broadcasting

When checking to see if two arrays have the same shape or have compatible numpy starts with the rightmost dimension and works its way left comparing them element-wise. For two dimensions to be compatible and therefore be broadcasted the following conditions need to be met for the pairs of dimensions:

The dimensions are equal.
One of the dimensions is 1 and the other is 1 (first condition) or more.

Info

Arrays do not need to have the same number of dimensions. For example if you have an RGB image so a 256x256x3 array of intensity values, and you want to scale each color (red, green, blue) in the image by a different value, you can multiply the image by a one-dimensional array with 3 values.

Image  (3d array): 256 x 256 x 3
Scale  (1d array):             3
Result (3d array): 256 x 256 x 3

Example

The following more complex example can still be broadcast.

A      (4d array):  8 x 1 x 6 x 1
B      (3d array):      7 x 1 x 5
Result (4d array):  8 x 7 x 6 x 5

Outer Product Using Broadcasting

Broadcasting provides a convenient way of taking the outer product of two vectors.

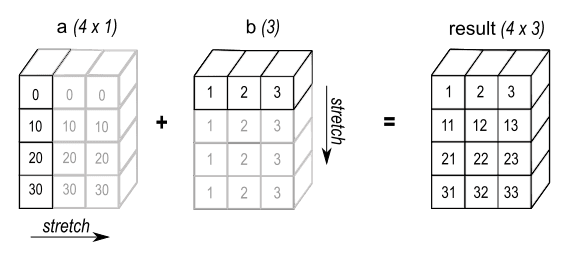
The efficient calculation of the outer product of two vectors with broadcasting.

a = np.array([0.0, 10.0, 20.0, 30.0]).reshape((4,1))
b = np.array([1.0, 2.0, 3.0]).reshape((1,3))
a*b

    array([[ 0.,  0.,  0.],
           [10., 20., 30.],
           [20., 40., 60.],
           [30., 60., 90.]])

However, it is not limited to the outer product of two vectors, it can be used to compute any outer product of two tensors.

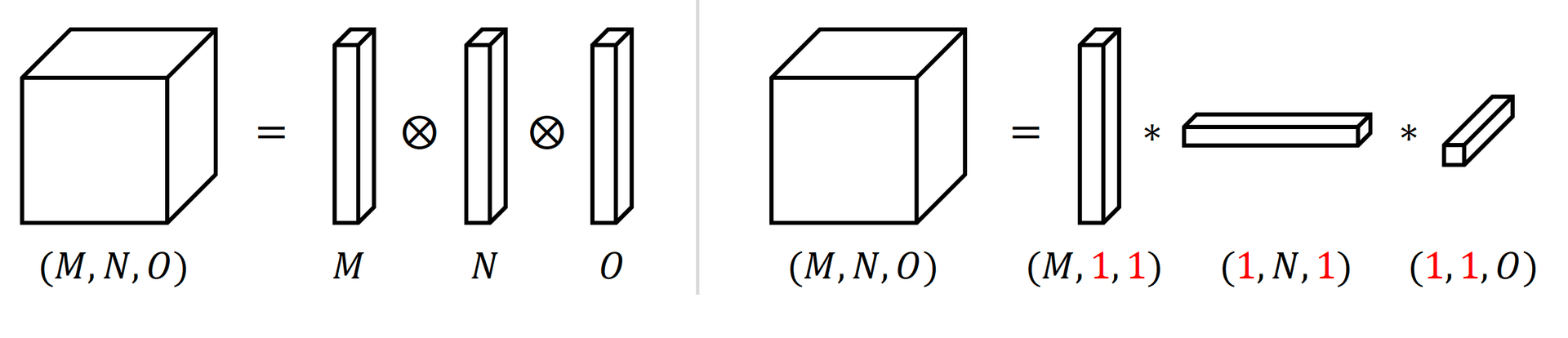
Using three vectors to calculate a 3D tensor.

c = np.array([1.0, 2.0, 3.0])
a = a.reshape((4,1,1))
b = b.reshape((1,3,1))
c= c.reshape(1,1,3)
a*b*c

    array([[[  0.,   0.,   0.],
            [  0.,   0.,   0.],
            [  0.,   0.,   0.]],
    
           [[ 10.,  20.,  30.],
            [ 20.,  40.,  60.],
            [ 30.,  60.,  90.]],
    
           [[ 20.,  40.,  60.],
            [ 40.,  80., 120.],
            [ 60., 120., 180.]],
    
           [[ 30.,  60.,  90.],
            [ 60., 120., 180.],
            [ 90., 180., 270.]]])

Cross Product Combinatorics