Analysis of Algorithms

One of the first lectures you will have as a computer scientist is "Algorthims and Data Structures" where one of the introductory topics is the analysis of algorithms. This is a crucial subject because it allows us to compare different algorithms and design new ones by identifying areas for improvement. To determine which algorithm is better and which areas to optimize, we need a systematic way to analyze them.

This can be done by running the algorithm on inputs of various sizes and benchmarking them. However, such benchmarking is highly dependent on the hardware and software environments where the algorithm runs. Thus, a more abstract approach is needed, where we analyze algorithms in terms of time and space complexity which focuses on how an algorithm behaves as the input size grows.

In time complexity analysis, we measure the number of basic operations an algorithm performs relative to the size of the input, often focusing on the worst-case scenario. While some operations like addition may be considered "cheap" or fast, we focus on more expensive operations like multiplications, comparisons, and data movements (e.g., swaps). For example on the Intel Sandy Bridge(2011-2013) an addition is 3 cycles, and a multiplication is 5. However, this can change with different hardware and depends if SIMD instructions are used which can do multiple operations in parallel.

Similarly, space complexity measures the amount of memory an algorithm uses as the input size increases. For instance, an algorithm might use a constant amount of memory, or it might require additional memory proportional to the size of the input, such as a complete copy of the input data.

Asymptotic Analysis

We are primarily interested in how the time and space complexity of an algorithm grows as the input size increases, particularly in the worst case. To do this, we express the performance of the algorithm as a mathematical function and analyze its growth rate. The goal is to compare this growth rate with a set of standard growth functions, which are used as benchmarks. This is known as asymptotic analysis.

The most common growth functions, listed in increasing order of growth rate, are:

Constant: $O(1)$
Logarithmic: $O(\log n)$
Linear: $O(n)$
Log-linear: $O(n \log n)$
Quadratic: $O(n^2)$
Cubic: $O(n^3)$
Polynomial: $O(n^k)$
Exponential: $O(2^n)$
Factorial: $O(n!)$

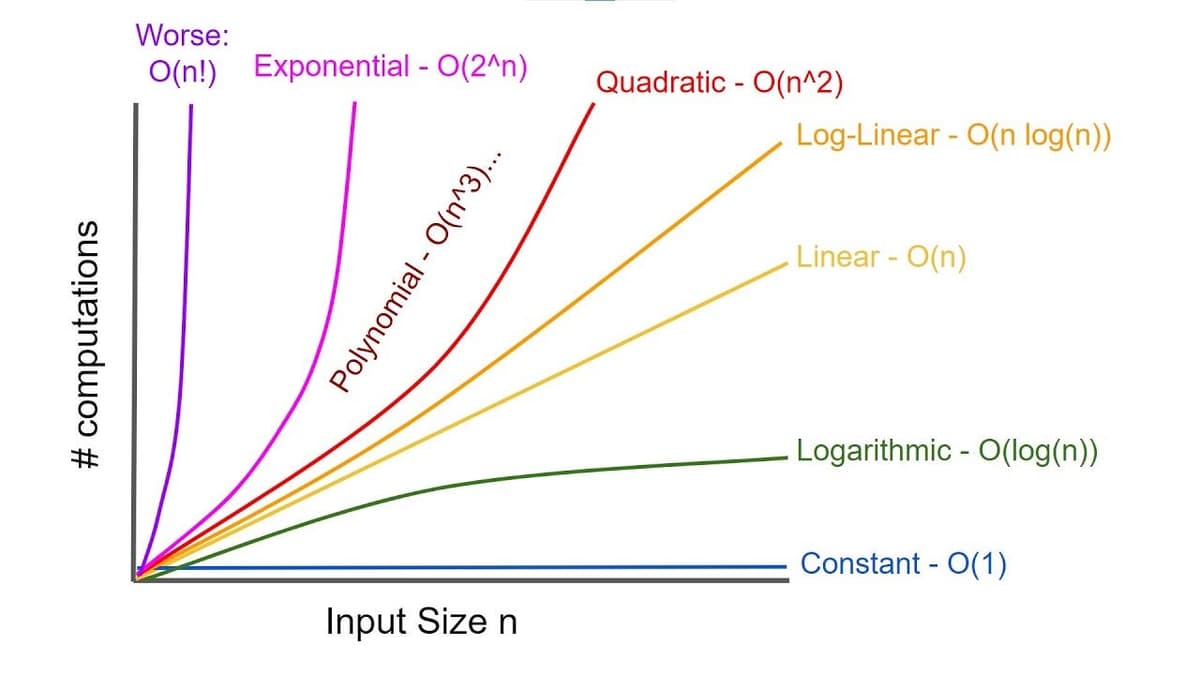
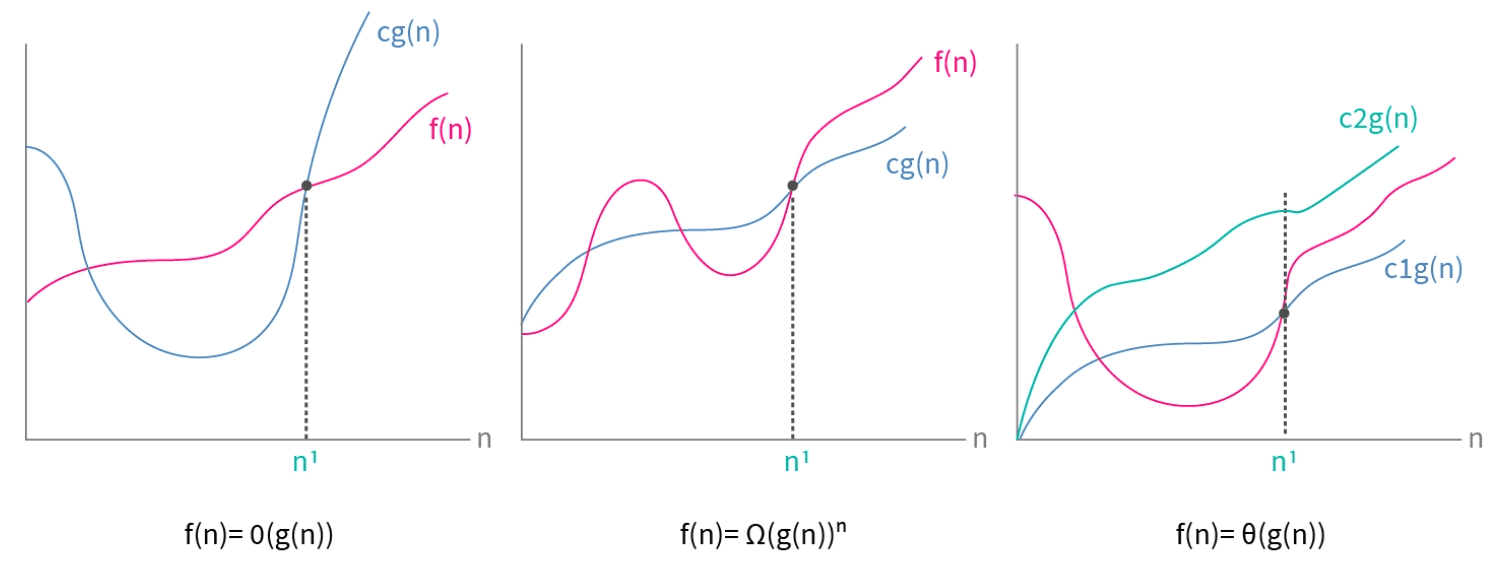
We can compare an algorithm's growth rate by determining which of these standard functions provides an upper bound. Specifically, if we have a function $f(n)$ that represents the algorithm's work, we determine the smallest standard function $g(n)$ such that $f(n)$ grows no faster than a constant multiple of $g(n)$ as $n$ becomes large. This is expressed as $f(n) \in O(g(n))$ often said as " $f(n)$ is big O of $g(n)$ " or " $f(n)$ is order of $g(n)$ " and called Big O notation.

Big O Notation

The formal definition of Big O notation is as follows:

A function $f(n)$ is said to be in $O(g(n))$ , if there exist constants $c > 0$ and $n_0 > 0$ such that:

f(n) \leq c \cdot g(n) \text{ for all } n \geq n_0

In simple terms, at some point $n_0$ the function $f(n)$ will always be less than or equal to $c \cdot g(n)$ for all $n > n_0$ .

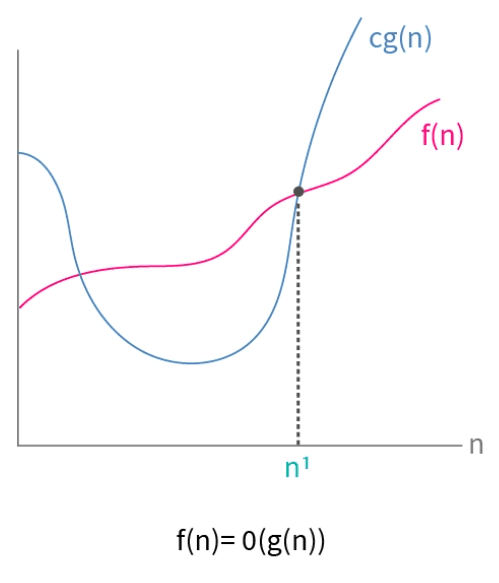
This method works because if we can find some $c$ and $n_0$ that satisfy the inequality, then we can also find different $c'$ and $n_0'$ that also satisfy the inequality as $n$ grows to infinity. This is because the function $g(n)$ grows faster than $f(n)$ so we can always find a $c'$ and $n_0'$ that satisfy the inequality, making the function $g(n)$ an upper bound on the growth rate of $f(n)$ . For this reason most students remember the following definition of Big O notation:

Suppress the lower order terms and constants to get the time complexity of the algorithm.

Example

We want to show that $f(n) = 5n^2 + 3n + 7$ is in $O(n^2)$ . For this we need to find constants $c$ and $n_0$ such that $f(n) \leq c \cdot n^2$ for all $n \geq n_0$ . We can see that as $n$ grows the $5n^2$ term will dominate the other terms so we can choose $c = 6$ and $n_0 = 1$ to satisfy the inequality:

5n^2 + 3n + 7 \leq 6n^2 \text{ for all } n \geq 1

Therefore, $f(n) = 5n^2 + 3n + 7$ is in $O(n^2)$ . But we could also choose $c = 7$ and $n_0 = 1$ to satisfy the inequality:

5n^2 + 3n + 7 \leq 7n^2 \text{ for all } n \geq 1

This is why we suppress the lower order terms and constants to get the time complexity of the algorithm. Let's also show that $f(n) = n^3 -n$ is in $O(n^3)$ . We can choose $c = 2$ and $n_0 = 1$ to satisfy the inequality or $c = 3$ and $n_0 = 1$ .

n^3 - n \leq 2n^3 \text{ for all } n \geq 1

Info

Why is exponential just $2^n$ not any other base like $3^n$ ?

The reason is that the base of the exponential function does not matter when we are talking about the order of growth. Different bases can be converted to each other by a constant factor, so they are considered equivalent. For example, $3^n = (2^{log_2(3)})^n = 2^{n \cdot log_2(3)}$ and because $log_2(3)$ is a constant it can be absorbed into the constant factor and we can just say that $3^n$ is $O(2^n)$ .

But why is $n^3$ then not $O(n^2)$ ? Because the base of the polynomial function does matter. The difference between $n^2$ and $n^3$ is not just a constant factor, but a factor of $n$ because $n^3 = n \cdot n^2$ .

Telescoping

To be able to find the time complexity of an algorithm we need to be able to express the time complexity as a function of the input size $n$ . Most of the time the algorithm can be expressed as a reccurance relation, i.e. a function that calls itself with a smaller input size. These reccurance relations are actually just some series, i.e a sum of terms. For example the reccurance relation $T(n) = T(n-1) + 2n$ with $T(0) = 0$ is just the sum of the first $n$ even numbers.

Telescoping is then a method to solve these series/reccurance relations to find a closed form solution, i.e. a function that gives the sum of the series. This closed form solution can then be used to find the time complexity of the algorithm. The idea of telescoping is to write out the series for a few terms and then find a pattern to simplify or cancel out terms. Once we have our closed form we can check it is correct using proof by induction.

Example

Lets show that the reccurance relation $T(n) = T(n-1) + 2n$ with $T(0) = 0$ is a sum of terms and can be solved using telescoping. The first step is to write out the first few expansions of the reccurance relation, it can also be helpful to write out the expansion step $k$ before the term:

\begin{align*} k=1 \quad T(n) &= \textcolor{red}{T(n-1)} + 2n \\ k=2 \quad T(n) &= \textcolor{red}{T(n-2) + 2(n-1)} + 2n \\ & = \textcolor{green}{T(n-2)} + 2(2n) - 2 \\ k=3 \quad T(n) &= \textcolor{green}{T(n-3) + 2(n-2)} + 2(2n) - 2 \\ &= \textcolor{orange}{T(n-3)} + 3(2n) - 4 - 2 \\ k=4 \quad T(n) &= \textcolor{orange}{T(n-4) + 2(n-3)} + 3(2n) - 4 - 2 \\ &= T(n-4) + 4(2n) - 6 - 4 - 2 \\ \end{align*}

Now we can see there is a pattern, with the trickiest part being connecting the subractions to $k$ and $n$ , but we can see that for $k=2$ its $-2(1)$ for $k=3$ its $-2(2 + 1)$ and for $k=4$ its $-2(3 + 2 + 1)$ .

T(n-k) = T(n-k) + k(2n) - 2 \sum_{i=1}^{k-1} i

However, we don't want the k in our closed form. To remove it we need to know when the recursive call will reach the base case. This is when $n=0$ so $n-k=0$ and $k=n$ . We can then substitute $k=n$ into the formula above to get:

\begin{align*} T(n) = T(0) + n(2n) - 2 \sum_{i=1}^{n-1} i \\ T(n) = 0 + 2n^2 - 2 \sum_{i=1}^{n-1} i \\ T(n) = 2n^2 - 2 \left( \frac{n(n-1)}{2} \right) \\ T(n) = 2n^2 - n^2 + n \\ T(n) = n^2 + n \end{align*}

Now that we have our closed form solution we can check that it is correct using proof by induction.

Proof

Proof by induction that $T(n) = n^2 + n$ is the correct closed form solution to the reccurance relation $T(n) = T(n-1) + 2n$ with $T(0) = 0$ .

Base case: $T(0) = 0^2 + 0 = 0$ which is true.
Inductive hypothesis: Assume $T(k) = k^2 + k$ is true for some $k \geq 0$ .
Inductive step: Show that if the hypothesis is true for $k$ then it is also true for $k+1$ .

$T(k+1) = T(k) + 2(k+1) = k^2 + k + 2k + 2 = k^2 + 3k + 2 = (k+1)^2 + (k+1)$

Therefore, by induction $T(n) = n^2 + n$ is the correct closed form solution to the reccurance relation $T(n) = T(n-1) + 2n$ with $T(0) = 0$ .

Since we now have the correct closed form solution we can supress the lower order terms and constants to get the time complexity of the algorithm. In this case the time complexity is $O(n^2)$ .

Info

It is useful to remember some of the closed forms of common series like the sum of the first $n$ natural numbers to make telescoping easier.

\sum_{i=1}^{n} i = \frac{n(n+1)}{2}

But because we are subtracting the sum of the first $n-1$ natural numbers we can subtract the last $n$ from the closed form to get the sum of the first $n-1$ natural numbers:

\sum_{i=1}^{n-1} i = \frac{n(n+1)}{2} - n = \frac{n(n-1)}{2}

The same can be done for other variations of the sum of the first $n$ natural numbers

Standard Multiplication

A classic introductory example of time complexity analysis is the multiplication of two numbers. Everyone learns how to multiply two numbers in primary school. You start by multiplying each digit of the first number by each digit of the second number and then adding them together whilst making sure to shift the numbers to the left depending on the position of the digit. For simplicity, let's assume that the numbers are of the same length as we can always pad the shorter number with zeros. For negative numbers we just need to check if only one of the numbers is negative and then add a negative sign to the result.

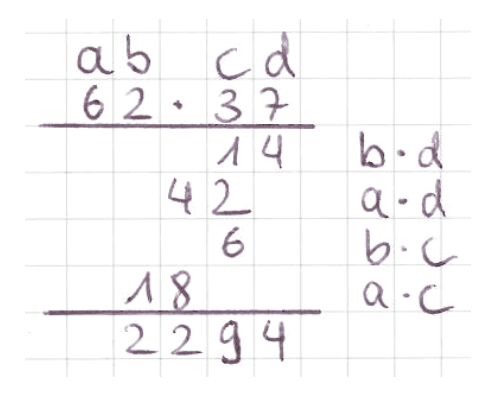
Multiplication of two numbers with 2 digits

If we only focus on counting the number of multiplications we can see that for two $n$ -digit we get the following pattern and closed form solution:

\begin{align*} T(1) &= 1 \\ T(2) &= 4 \\ T(3) &= 9 \\ T(4) &= 16 \\ T(n) &= n^2 \end{align*}

The pattern is quite obvious. In fact, you can also derive the recursive relation $T(n) = T(n-1) + 2n - 1$ with $T(1) = 1$ . Using telescoping, you can find the closed-form solution $T(n) = n^2$ .

This recursive relation makes sense if you think about multiplying two numbers recursively. For example, in multiplying $123 \cdot 456$ , you have $T(2)$ multiplications for $23 \cdot 56$ , and then you add another $n-1$ multiplications to handle the interaction between the leading digits (e.g., 4 with 23) and finally $n$ multiplications to multiply the leading digit (1) with the entire second number.

From the closed-form solution, we can quickly see that the time complexity of standard multiplication is $O(n^2)$ . We can set $c = 1$ and $n_0 = 1$ to satisfy the inequality $T(n) \leq c \cdot n^2$ for all $n \geq n_0$ .

Karatsuba Algorithm

The Karatsuba algorithm, named after Anatolii Karatsuba, was discovered in 1960 and revolutionized the multiplication of large numbers. Before Karatsuba's work, it was generally believed that $O(n^2)$ was the best possible time complexity for multiplying two numbers. However, with Karatsuba's algorithm demonstrated it is possible to perform multiplication faster than the standard approach by reducing the number of multiplicative operations at the expense of a few more additions which are considered by far cheaper on most hardware.

The Karatsuba algorithm uses a divide and conquer approach, splitting each number into two smaller parts, multiplying them recursively, and combining the results in a clever way to remove a multiplication operation. The algorithm is as follows for multiplying two $n$ -digit numbers $x$ and $y$ where we assume $n$ is a power of 2 for easier splitting:

(10^{n/2}a + b)(10^{n/2}c + d) = 10^n \textcolor{red}{a \cdot c} + 10^{n/2} \textcolor{red}{a \cdot c} + 10^{n/2} \textcolor{green}{b \cdot d} + \textcolor{green}{b \cdot d} + 10^{n/2} \textcolor{orange}{(a - b) \cdot (d - c)}

Where $a$ and $b$ are the first and second half of $x$ and $c$ and $d$ are the first and second half of $y$ . The algorithm then recursively calculates the following three multiplications recursively:

$\textcolor{red}{a \cdot c}$
$\textcolor{green}{b \cdot d}$
$\textcolor{orange}{(a - b) \cdot (d - c)}$

Karatsuba algorithm for multiplying two numbers.

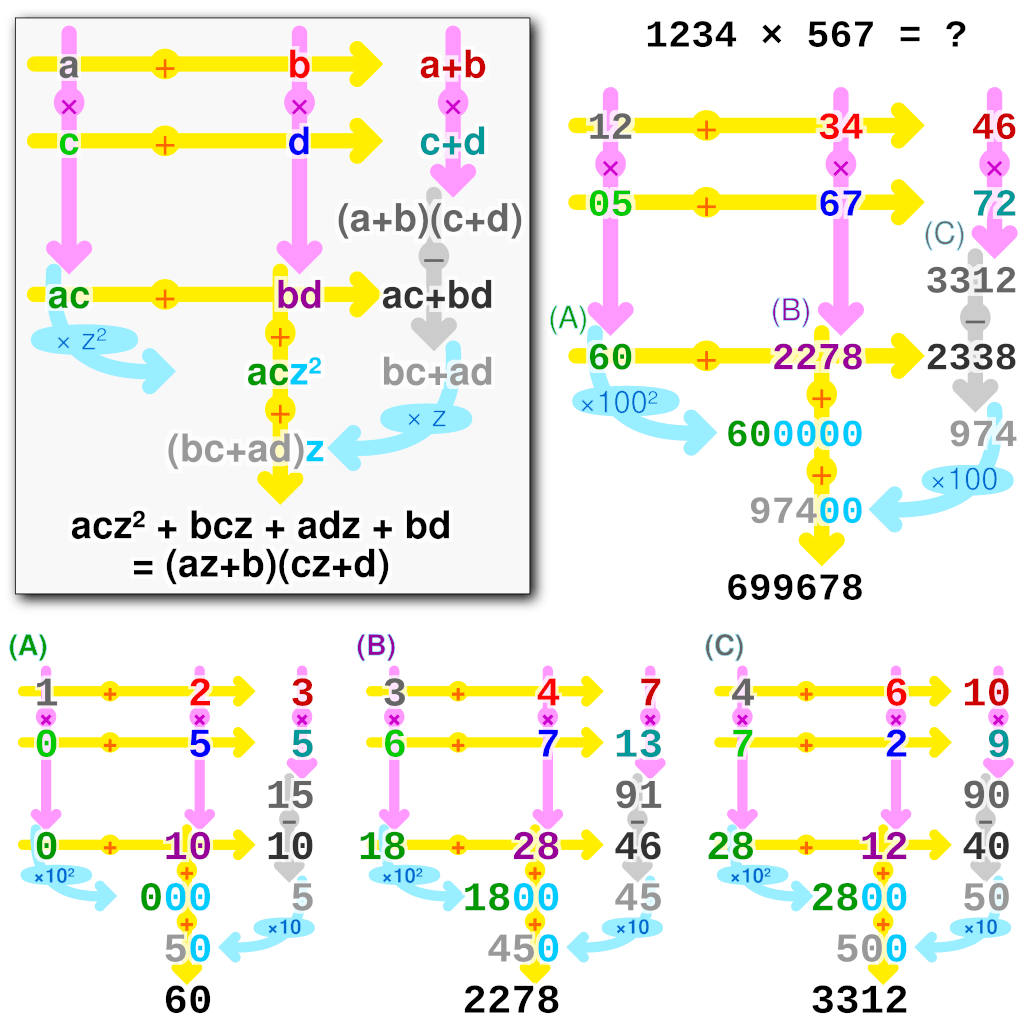
We can quiet easily see that the reccurance relation for the Karatsuba algorithm is as follows if we only focus on the number of multiplications:

T(2^k) = \begin{cases} 1 & \text{if } k = 0 \\ 3T(2^{k-1}) & \text{if } k > 0 \end{cases}

This is because for the base case where $n=1$ so $k=0$ we only need 1 multiplication and then if we want to multiply two numbers with two digits we need to perform 3 multiplications and then for two numbers with 4 digits we need to perform 3 times a multiplication of two numbers with 2 digits etc. Using telescoping we can find the closed form solution and then show the time complexity of the Karatsuba algorithm.

\begin{align*} l=1 \quad T(2^k) &= 3T(2^{k-1}) \\ l=2 \quad T(2^k) &= 3(3T(2^{k-2})) = 3^2T(2^{k-2}) \\ l=3 \quad T(2^k) &= 3^2(3T(2^{k-3})) = 3^3T(2^{k-3}) \\ l=4 \quad T(2^k) &= 3^3(3T(2^{k-4})) = 3^4T(2^{k-4}) \\ \end{align*}

We can see the pattern is as follows:

T(2^k) = 3^kT(2^0) = 3^k

Proof

Proof by induction that $T(2^k) = 3^k$ is the correct closed form solution to the reccurance relation $T(2^k) = 3T(2^{k-1})$ with $T(1) = 1$ .

Base case: $T(1) = T(2^0) = 1 = 3^0$ which is true.
Inductive hypothesis: Assume $T(2^k) = 3^k$ is true for some $k \geq 0$ .
Inductive step: Show that if the hypothesis is true for $k$ then it is also true for $k+1$ .

$T(2^{k+1}) = 3T(2^k) = 3 \cdot 3^k = 3^{k+1}$

Therefore, by induction $T(2^k) = 3^k$ is the correct closed form solution to the reccurance relation $T(2^k) = 3T(2^{k-1})$ with $T(1) = 1$ .

However, we want the time complexity in terms of $n$ not $k$ so we need to find the relationship between $n$ and $k$ . We know that $n = 2^k$ so $k = \log_2 n$ . We can then substitute $k = \log_2 n$ and use the fact that any number can be written as $a^{\log_a b} = b$ and the Logarithmic identity $\log_a b \cdot \log_b a = 1$ to get the time complexity in terms of $n$ :

T(n) = 3^{\log_2 n} = (2^{\log_2 3})^{\log_2 n} = 2^{\log_2 3 \cdot \log_2 n} = n^{\log_2 3} \approx n^{1.58}

Therefore, the time complexity of the Karatsuba algorithm is $O(n^{1.58})$ which is faster than the standard multiplication algorithm with time complexity $O(n^2)$ .

Example

Let's first show how it works for multiplying two 2-digit numbers $23 \cdot 56$ so where $n=1$ and $a=2$ , $b=3$ , $c=5$ and $d=6$ .

\begin{align*} 62 \cdot 37 &= (10^{2/2} \cdot 6 + 2)(10^{2/2} \cdot 3 + 7) \\ &= 10^2 \textcolor{red}{6 \cdot 3} + 10^{2/2} \textcolor{red}{6 \cdot 3} + 10^{2/2} \textcolor{green}{2 \cdot 7} + \textcolor{green}{2 \cdot 7} + 10^{2/2} \textcolor{orange}{(6 - 2) \cdot (7 - 3)} \\ &= 10^2 \cdot \textcolor{red}{18} + 10^{2/2} \cdot \textcolor{red}{18} + 10^{2/2} \cdot \textcolor{green}{14} + \textcolor{green}{14} + 10^{2/2} \cdot \textcolor{orange}{16} \\ &= 1800 + 180 + 140 + 14 + 160 \\ &= 2294 \end{align*}

If we now use the Karatsuba algorithm to multiply two 4-digit numbers $6237 \cdot 5898$ it get's a bit more complicated by hand but the algorithm is the same. We split the numbers into two parts and then recursively multiply them:

\begin{align*} 6237 \cdot 5898 &= (10^{4/2} \cdot 62 + 37)(10^{4/2} \cdot 58 + 98) \\ &= 10^4 \textcolor{red}{62 \cdot 58} + 10^{4/2} \textcolor{red}{62 \cdot 58} + 10^{4/2} \textcolor{green}{37 \cdot 98} + \textcolor{green}{37 \cdot 98} + 10^{4/2} \textcolor{orange}{(62 - 37) \cdot (98 - 58)} \\ \textcolor{red}{62 \cdot 58} &= 10^2 6 \cdot 5 + 10^1 6 \cdot 5 + 10^1 2 \cdot 8 + 2 \cdot 8 + 10^1 (6 - 2) \cdot (8 - 5) \\ &= 3000 + 300 + 160 + 16 + 120 \\ &= 3596 \text{... and so on for the other recursive multiplications} \end{align*}

Big Omega and Big Theta

Unlike Big O which is an upper bound on the growth rate of a function, Big Omega is a lower bound on the growth rate of a function. In simpler terms, Big Omega is used to describe the best-case scenario of an algorithm. More formally, a function $f(n)$ is said to be in $\Omega(g(n))$ where $g(n)$ is a growth function and the following condition is satisfied for all $n > n_0$ :

f(n) \in \Omega(g(n)) \iff \exists c > 0, n_0 > 0 \text{ such that } f(n) \geq c \cdot g(n)

Big Theta combines the concepts of Big O and Big Omega. It is used to describe the tight bound on the growth rate of a function meaning it gives both an upper and lower bound on the growth rate of a function. More formally, a function $f(n)$ is said to be in $\Theta(g(n))$ where $g(n)$ is a growth function and the following condition is satisfied for all $n > n_0$ :

f(n) \in \Theta(g(n)) \iff \exists c_1, c_2 > 0, n_0 > 0 \text{ such that } c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)

Master Theorem

The master theorem is a formula for quickly determining the time complexity of divide-and-conquer algorithms. More specifically, it determines the tight asymptotic bound theta $\Theta(g(n))$ for the time complexity of an algorithm that can be expressed as a reccurance relation. It requires the reccurance relation to be in a specific form, but if it is then the time complexity can be determined by just simply looking at the reccurance relation and extracting parameters from it. The reccurance relation needs to be in the form:

T(n) = aT\left(\frac{n}{b}\right) + f(n)

We can then determine the time complexity of the algorithm by looking at the parameters $a$ , $b$ and the function $f(n)$ . We also need to calculate the following value which is the relationship between the number of subproblems and the size of the subproblems:

c_{\text{crit}} = \log_b a = \frac{\log_2 a}{\log_2 b} = \frac{\text{log of # subproblems}}{\text{log of relative size of subproblems}}

The master theorem then determines the time complexity based on the following three cases:

Doesnt work for all cases, like fibonacci. Solve using telescoping.

Average Case Analysis

Using probability to find the average case time complexity of an algorithm. Seems annoying. Shows that the average case time complexity of quicksort is $O(n \log n)$ .

Amortized Analysis

Accounting Method

My Digital Garden What is NP-Hard?